درس 2: تابع درجه سوم، توابع یکنوا و بخش‌پذیری و تقسیم
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
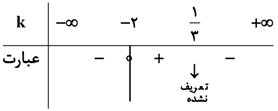
بزرگ‌ترین بازه برای $k$ که در آن تابع نمایی $y={{\left( \frac{5-k}{1-3k} \right)}^{x}}$ همواره اکیداً صعودی باشد، کدام است؟
1 )
$\left( -1,\frac{1}{3} \right)$
$\left( -2,\frac{1}{3} \right)$
3 )
$\left( -3,\frac{1}{3} \right)$
4 )
$\left( -4,\frac{1}{3} \right)$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...