در مثلث شکل مقابل طول نیمساز زاویهٔ چقدر است؟ | هندسه (2) یازدهم شماره 65831 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

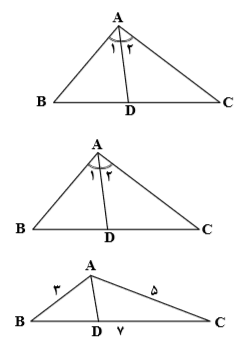
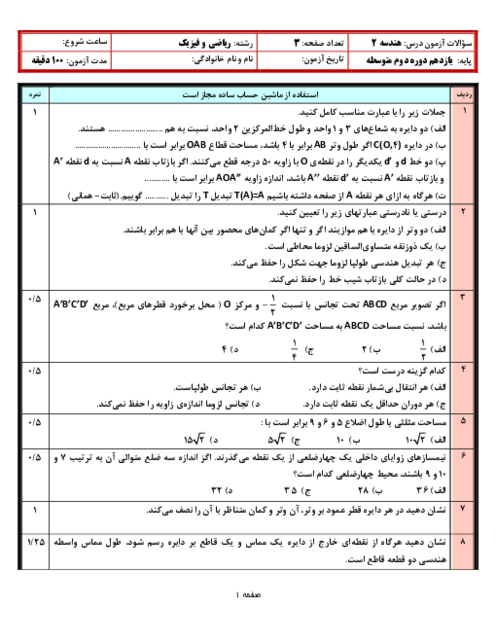
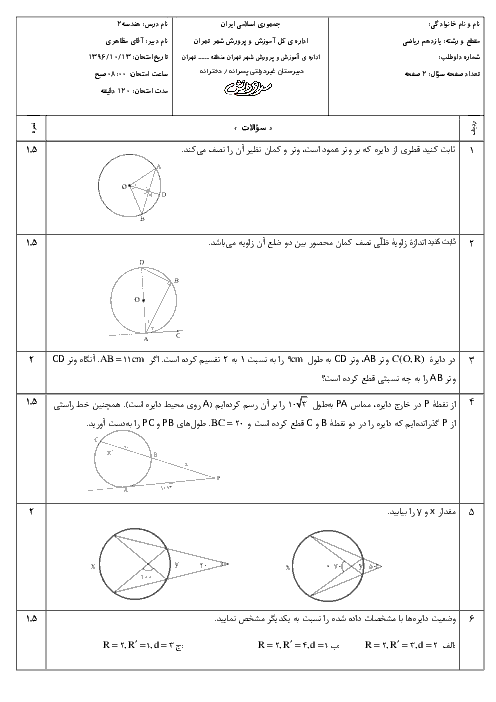
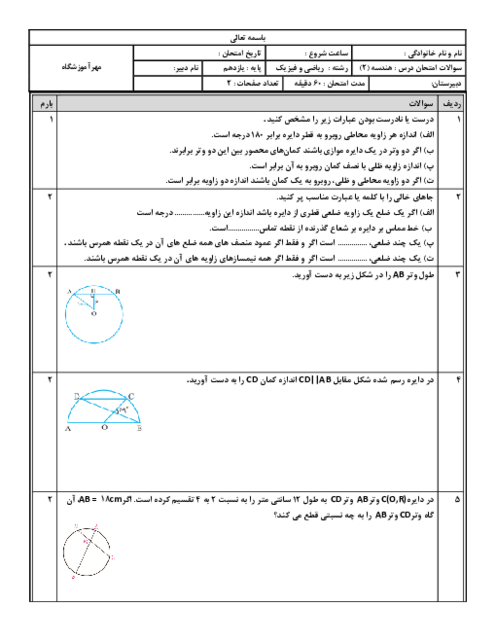
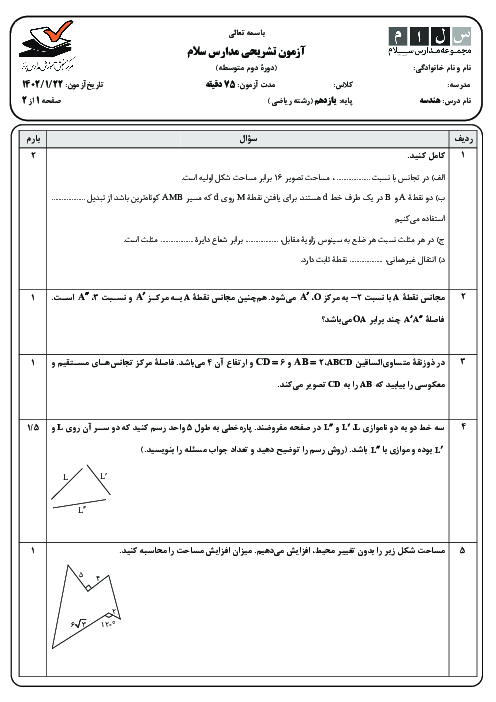
درس 3: قضیۀ نیمسازهای زوایای داخلی و محاسبۀ طول نیمسازها هندسه (2) یازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

در مثلث شکل مقابل طول نیمساز زاویهٔ $A$ چقدر است؟

1 )

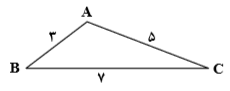
$\frac{15}{8}$

2 )

$\frac{21}{8}$

3 )

$\frac{35}{8}$

4 )

$\frac{25}{8}$

نمایش پاسخ

نکته (قضیهٔ نیمساز): در هر مثلث، نیمساز هر زاویهٔ داخلی، ضلع روبه‌رو به‌ آن زاویه را به‌نسبت اندازه‌های اضلاع آن زاویه تقسیم می‌کند.

${{\hat{A}}_{1}}={{\hat{A}}_{2}}\Rightarrow \frac{BD}{CD}=\frac{AB}{AC}$

نکته: در مثلث دلخواه $ABC$ اگر $AD$ نیمساز زاویهٔ داخلی $A$ باشد، داریم:

$A{{D}^{2}}=AB\cdot AC-BD\cdot DC$

ابتدا به کمک قضیهٔ نیمساز طول پاره‌خط‌های $BD$ و $CD$ را حساب می‌کنیم:

$\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow \frac{3}{5}=\frac{BD}{7-BD}\Rightarrow 5BD=21-3BD\Rightarrow BD=\frac{21}{8}\Rightarrow CD=\frac{35}{8}$

اکنون طول نیمساز $AD$ را محاسبه می‌کنیم:

$A{{D}^{2}}=3\times 5=\frac{35}{8}\times \frac{21}{8}\Rightarrow A{{D}^{2}}=15-15\times \frac{49}{64}\Rightarrow A{{D}^{2}}=15(1-\frac{49}{64})$

$\Rightarrow A{{D}^{2}}=15\times \frac{15}{64}\Rightarrow A{{D}^{2}}={{(\frac{15}{8})}^{2}}\Rightarrow AD=\frac{15}{8}$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1402/06/26

عباس ابراهیمی علویجه

محتوای متنی دوره آموزشی، هندسه (2) یازدهم دوره دوم متوسطه- نظری

مدرس: جابر عامری

مدت دوره: 162 صفحه (3 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

سوپراستار

کلید طلایی نمره 20 در امتحان هماهنگ کشوری هندسه 2 یازدهم رشته ریاضی فیزیک

51 صفحه

کلید طلایی نمره 20 در امتحان هماهنگ کشوری هندسه 2 یازدهم رشته ریاضی فیزیک

کلاس یازدهمی

نمونه سوال امتحان شبه نهایی هندسه 2 استان خراسان رضوی خرداد 1403

6 صفحه

نمونه سوال امتحان شبه نهایی هندسه 2 استان خراسان رضوی خرداد 1403

مهدی کلاهی

رایـــــگان

آزمون نوبت دوم هندسه (2) یازدهم دبیرستان موحد | خرداد 1398 + پاسخ

1 صفحه

آزمون نوبت دوم هندسه (2) یازدهم دبیرستان موحد | خرداد 1398 + پاسخ

عباس رحمتی

رایـــــگان

آزمون نوبت اول هندسه (2) یازدهم دبیرستان انرژی اتمی | دی 1396

6 صفحه

آزمون نوبت اول هندسه (2) یازدهم دبیرستان انرژی اتمی | دی 1396

مریم صادق

سوالات آزمون نوبت اول هندسه (2) یازدهم دبیرستان محمدامین (ص) | دی 1400

4 صفحه

سوالات آزمون نوبت اول هندسه (2) یازدهم دبیرستان محمدامین (ص) | دی 1400

اردوان مختاری

رایـــــگان

آزمون آمادگی امتحان نوبت اول هندسه (2) پایه یازدهم ریاضی | دبیرستان سرای دانش واحد حافظ

5 صفحه

آزمون آمادگی امتحان نوبت اول هندسه (2) پایه یازدهم ریاضی | دبیرستان سرای…

کلاس یازدهمی

رایـــــگان

درسنامه آموزشی و 46 سوال تستی هندسه (2) پایه یازدهم رشته ریاضی | فصل اول- درس 1 و 2

20 صفحه

درسنامه آموزشی و 46 سوال تستی هندسه (2) پایه یازدهم رشته ریاضی | فصل اول-…

کلاس یازدهمی

سوالات آزمون نوبت اول هندسه (2) یازدهم دبیرستان شهید غفار زمانی | دی 1400

5 صفحه

سوالات آزمون نوبت اول هندسه (2) یازدهم دبیرستان شهید غفار زمانی | دی 1400

عباس ابراهیمی علویجه

آزمون هندسه 2 امتحانات دی ماه 1403 دبیرستان شهید هاشمی نژاد

5 صفحه

آزمون هندسه 2 امتحانات دی ماه 1403 دبیرستان شهید هاشمی نژاد

مجتبی محمدیان

نمونه سوال شبه نهایی نوبت دوم هندسه 2 پایه یازدهم رشته ریاضی استان خراسان رضوی

4 صفحه

نمونه سوال شبه نهایی نوبت دوم هندسه 2 پایه یازدهم رشته ریاضی استان خراسان…

مهدی کلاهی

موارد بیشتر

موارد بیشتر

ارسال فایل

در دایره‌ای به شعاع 12متر، طول کمانی از این دایره 9متر است. زاویه مرکزی مقابل به این کمان چند رادیان است؟

در شکل زیر مقدار a کدام است؟

طریقه محاسبه زوایا در اشکال داخل دایره چگونه است؟

موارد بیشتر

ارسال پرسش

موارد بیشتر