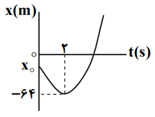
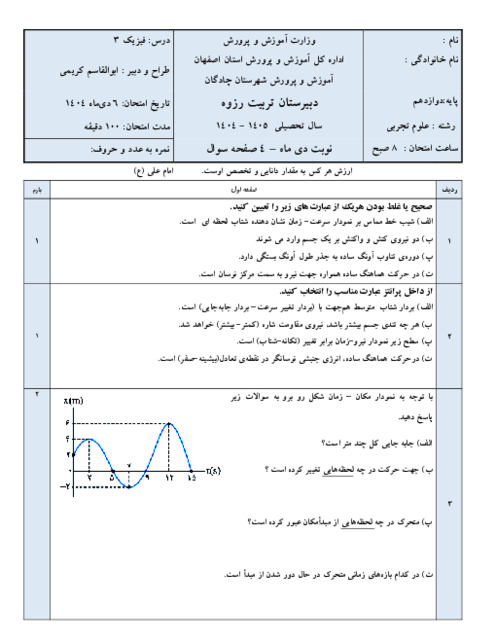
نمودار مكان - زمان متحركی كه با شتاب ثابت روی محور $x$ حركت می‌كند، مطابق شكل است. متحرک با تندی $۳۲\frac{m}{s}$ از مبدأ مكان عبور می‌كند. مكان اوليۀ متحرک $({{x}_{{}^\circ }})$ برحسب متر کدام است؟