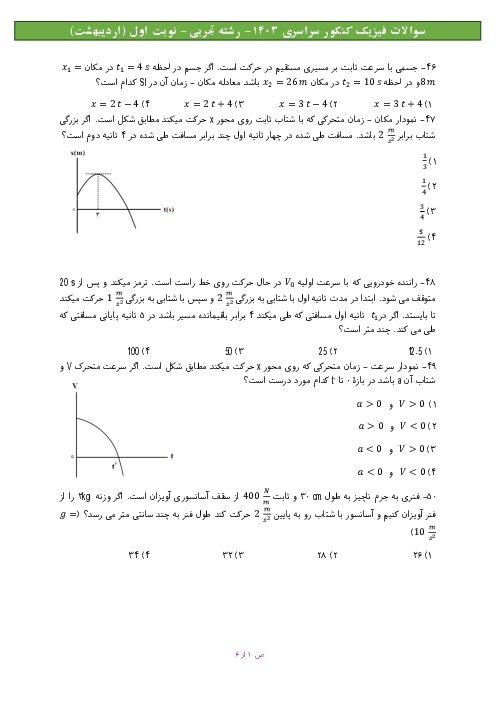
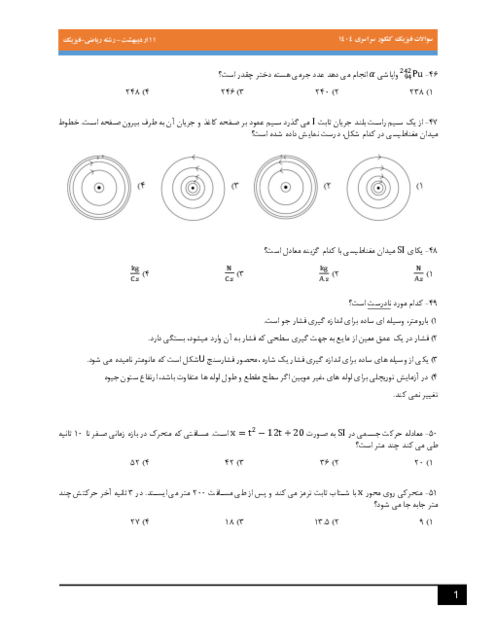
گام اول: مطابق شکل نیروهای وارد بر هر سه جسم را رسم می‌کنیم:
چون هر سه جسم در حالت تعادل قرار دارند برایند نیروهای وارد بر هر کدام برابر صفر است.

چوب: ${{F}_{b(1)}}={{W}_{1}}$

ظرف(کاسه): ${{F}_{b(2)}}={{W}_{2}}$

وزنه: ${{F}_{b(3)}}={{W}_{3}}-{{F}_{N}}$

از طرفی واکنش نیروهای شناوری ${{\overrightarrow{F}}_{b(1)}}$، ${{\overrightarrow{F}}_{b(2)}}$ و ${{\overrightarrow{F}}_{b(3)}}$ به آب وارد می‌شود. فشار در کف ظرف ناشی از فشار هوا، وزن آب درون ظرف و نیروهای ${{{F}'}_{b(1)}}$، ${{{F}'}_{b(2)}}$ و ${{{F}'}_{b(3)}}$ است، یعنی:

کف ظرف: $P={{P}_{{}^\circ }}+\frac{{{{{F}'}}_{b(1)}}+{{{{F}'}}_{b(2)}}+{{{{F}'}}_{b(3)}}}{A}={{P}_{{}^\circ }}+\frac{W+{{W}_{1}}+{{W}_{2}}+({{W}_{3}}-{{F}_{N}})}{A}$

گام دوم: اگر چوب را درون ظرف (کاسه) قرار دهیم، مجموعهٔ چوب و کاسه همچنان روی سطح آب شناور می‌ماند بنابراین نیروی شناوری وارد بر این دو جسم برابر مجموع وزن آن‌ها است.

${{F}_{b(1,2)}}={{W}_{1}}+{{W}_{2}}$

و فشار در کف ظرف برابر است با:

$P={{P}_{{}^\circ }}+\frac{W+{{{{F}'}}_{b(1,2)}}+{{{{F}'}}_{b(3)}}}{A}={{P}_{{}^\circ }}+\frac{W+{{W}_{1}}+{{W}_{2}}+({{W}_{3}}-{{F}_{N}})}{A}$

همان‌طور که ملاحظه می‌کنید فشار در کف ظرف نسبت به حالت اولیه تغییر نکرد.
گام سوم: در حالت دوم وزنه را درون ظرف (کاسه) قرار می‌دهیم. در این حالت با توجه به شناوربودن مجموعهٔ وزنه و کاسه در سطح آب می‌توان گفت:

${{F}_{b(1,3)}}={{W}_{1}}+{{W}_{3}}$

$P={{P}_{{}^\circ }}+\frac{W+{{{{F}'}}_{b(2)}}+{{{{F}'}}_{b(1,3)}}}{A}={{P}_{{}^\circ }}+\frac{W+{{W}_{1}}+{{W}_{2}}+{{W}_{3}}}{A}$

با توجه به نتیجهٔ به دست آمده، در این حالت (چون نیروی ${{F}_{N}}$ حذف می‌شود) فشار در کف ظرف افزایش می‌یابد.