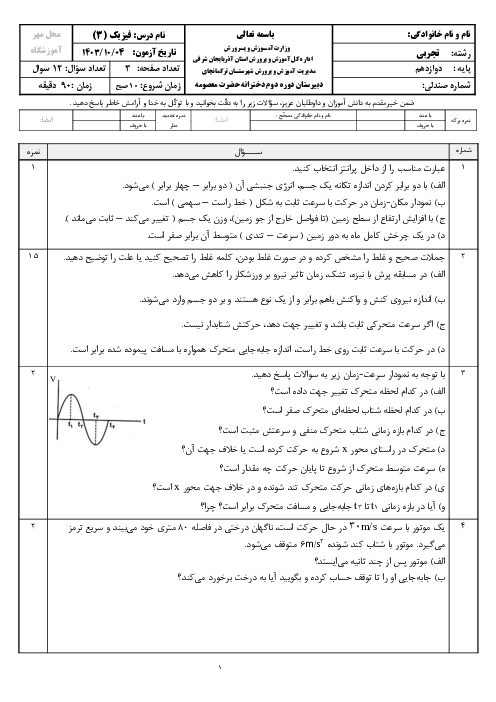
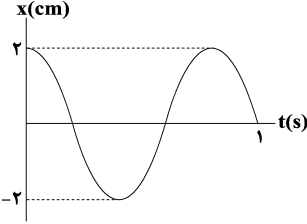
نمودار مکان ـ زمان یک آونگ که در سطح زمین حرکت هماهنگ ساده انجام میدهد مطابق شکل زیر است. اگر این آونگ را به سیارهای ببریم که شتاب گرانش در سطح آن $\frac{1}{4}$ برابر شتاب گرانش در سطح زمین باشد، بسامد زاویهای آونگ در سیارۀ جدید چند رادیان بر ثانیه است؟
1 )
$\frac{2\pi }{5}$
$\frac{5\pi }{4}$
3 )
$\frac{5\pi }{2}$
4 )
$\frac{4\pi }{5}$