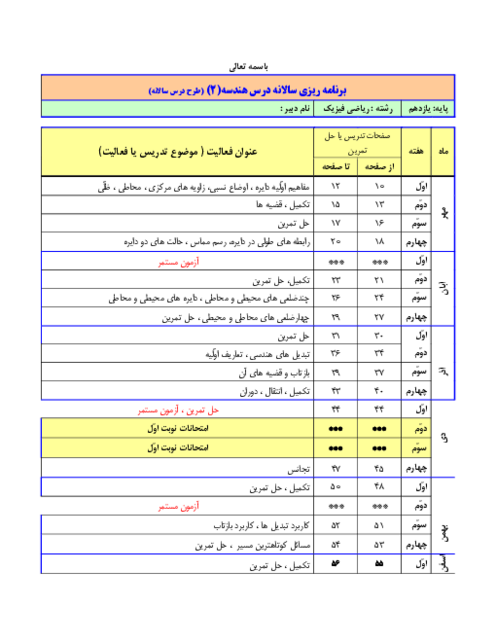
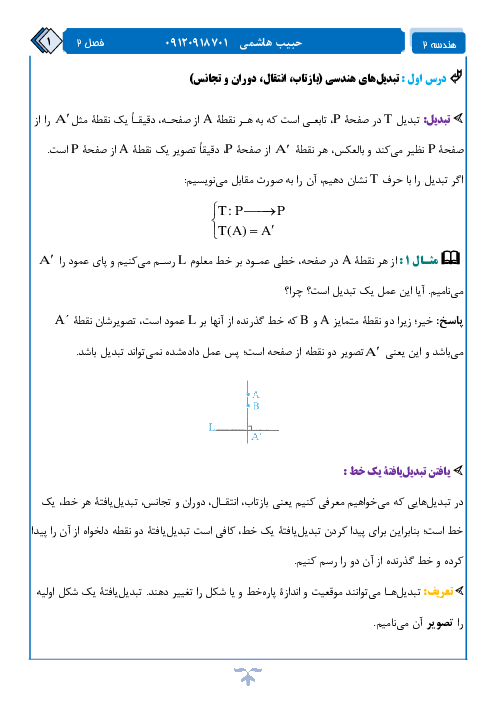
** فصل 2: تبدیل‌های هندسی و کاربردها
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
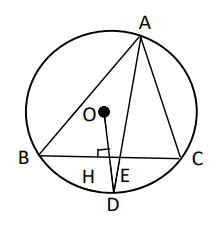
در شکل مقابل، O مرکز دایره و OD عمود بر BC است. اگر $3AB = 4AC$ باشد، حاصل $\frac{{HE}}{{BC}}$ کدام است؟
1 )
$\frac{2}{{14}}$
2 )
$\frac{1}{{7}}$
3 )
$\frac{2}{{9}}$
$\frac{1}{{14}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...