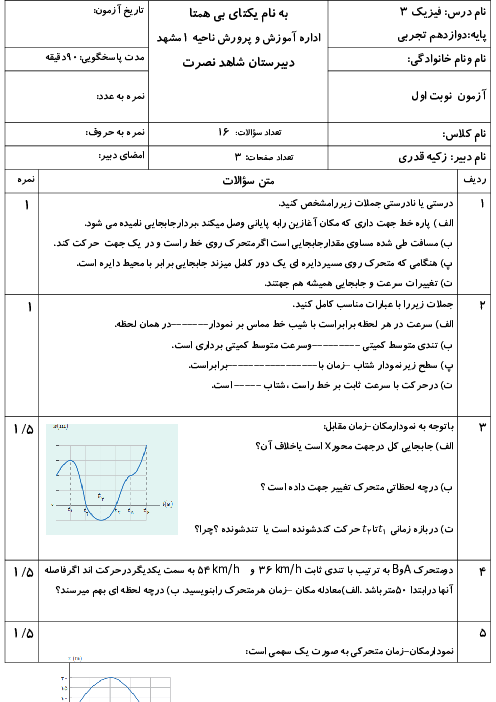
مادامی‌كه جهت حركت نوسانگر تغيير نمی‌كند تندی متوسط و اندازهٔ سرعت متوسط با يكديگر برابر است بنابراين فرض می‌كنيم در لحظه‌ای كه تندی متوسط نوسانگر دو برابر بزرگی سرعت متوسط آن است نوسانگر در فاصلهٔ $a$ از نقطهٔ $C$ قرار دارد. 

$\frac{T}{4}=0/2s\Rightarrow T=0/8s\xrightarrow{\omega =\frac{2\pi }{T}}\omega =\frac{5\pi }{2}\frac{rad}{s}$

$\frac{{{S}_{av}}}{\left| {{v}_{av}} \right|}=2\xrightarrow[\left| {{v}_{av}} \right|=\frac{\left| \overrightarrow{d} \right|}{t}]{{{S}_{av}}=\frac{\ell }{t}}\frac{\ell }{\left| \overrightarrow{d} \right|}=2\xrightarrow[\left| \overrightarrow{d} \right|=2A-a]{\ell =2A+a}$

$\frac{2A+a}{2A-a}=2\Rightarrow 4A-2a=2A+a\Rightarrow a=\frac{2A}{3}$

$\Rightarrow x=\frac{2A}{3}-A=-\frac{A}{3}=-\frac{6}{3}=-2cm$

$\left| a \right|={{\omega }^{2}}\left| x \right|\xrightarrow[x=-2cm=-0/02m]{\omega =\frac{5\pi }{2}\frac{rad}{s}}\left| a \right|=\frac{25{{\pi }^{2}}}{4}\times 0/02=\frac{{{\pi }^{2}}}{8}\frac{m}{{{s}^{2}}}$