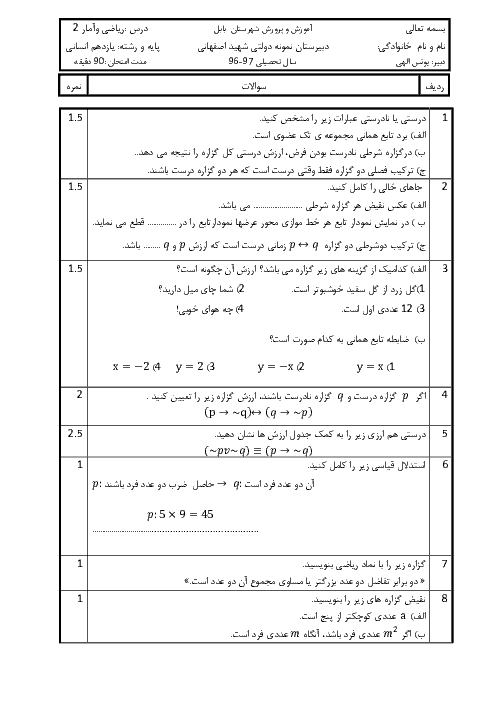
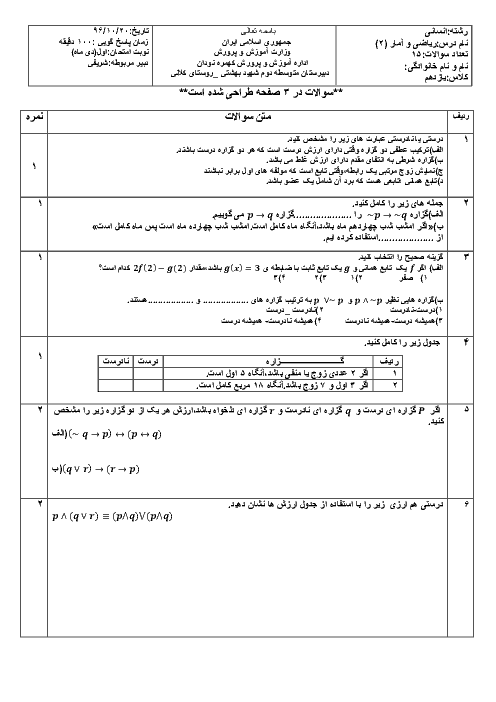
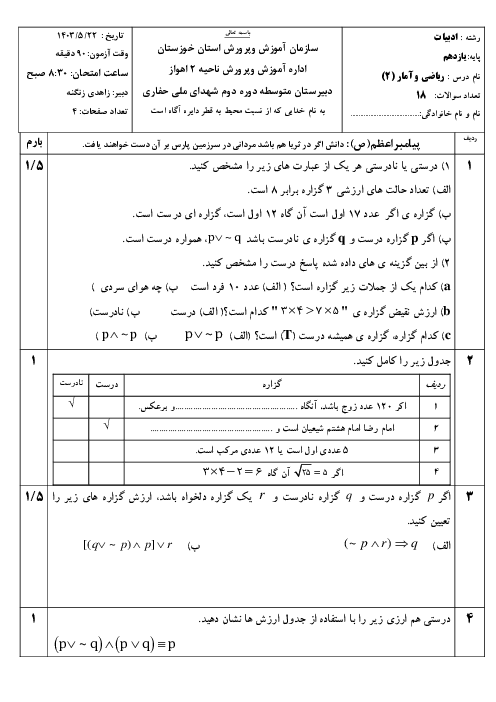
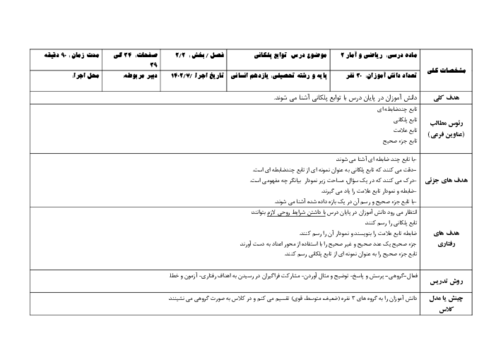
فصل 1: آشنایی با منطق و استدلال ریاضی
ریاضی و آمار (2)
یازدهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
چهار لیوان به صورت شکل زیر داریم که سه تا از آنها وارونه است. در هر حرکت مجاز هستیم دقیقاً دو لیوان را تغییر وضعیت دهیم. حداقل با چند حرکت مجاز میتوان هر چهار لیوان را در حالت درست (رو به بالا) قرار دارد؟
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!