** فصل 3: نوسان و امواج
فیزیک (3) تجربی
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
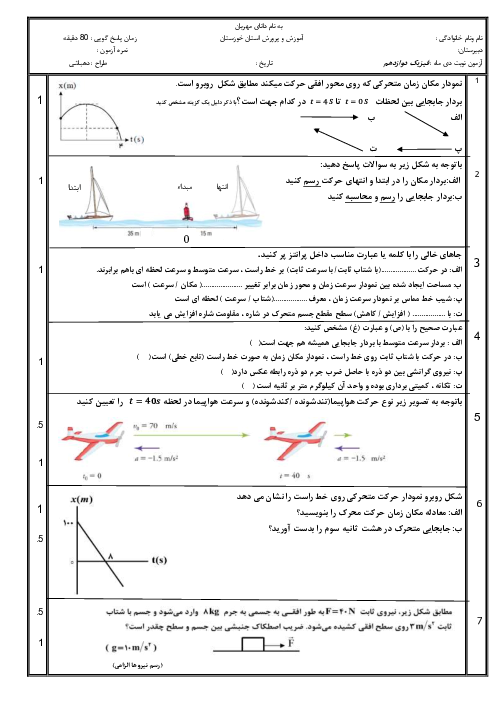
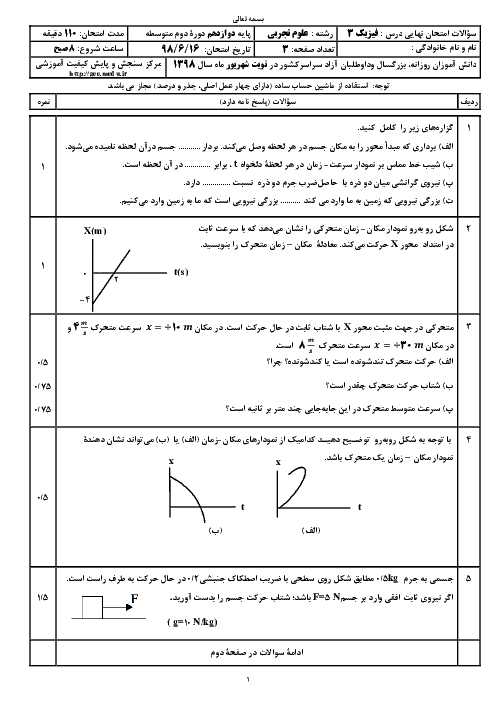
وزنه‌ای به جرم $200g$ به انتهای فنری با ثابت $3/2$ نیوتون بر سانتی‌متر بسته شده و مجموعه روی سطح افقی بدون اصطکاکی حرکت هماهنگ ساده انجام می‌دهد. اگر تندی بیشینهٔ وزنه $2/4$ متر بر ثانیه باشد، اختلاف بین حداکثر و حداقل طول فنر حین نوسان وزنه چند متر است؟
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...