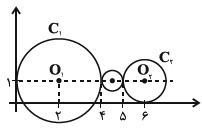
دو دایرهٔ ${{C}_{1}}={{x}^{2}}+{{y}^{2}}-4x-2y+1=0$ و ${{C}_{2}}={{x}^{2}}+{{y}^{2}}-12x-2y+36=0$ مفروض‌اند. معادلهٔ دایره‌ای که بر دایره‌های ${{C}_{1}}$ و ${{C}_{2}}$ مماس خارج بوده و مرکز آن روی خط‌المرکزین این دایره قرار داشته باشد، کدام است؟
1 )
${{(x-\frac{9}{2})}^{2}}+{{(y-1)}^{2}}=1$
2 )
${{(x-\frac{7}{2})}^{2}}+{{(y-1)}^{2}}=1$
${{(x-\frac{9}{2})}^{2}}+{{(y-1)}^{2}}=\frac{1}{4}$
4 )
${{(x-\frac{7}{2})}^{2}}+{{(y-1)}^{2}}=\frac{1}{4}$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...