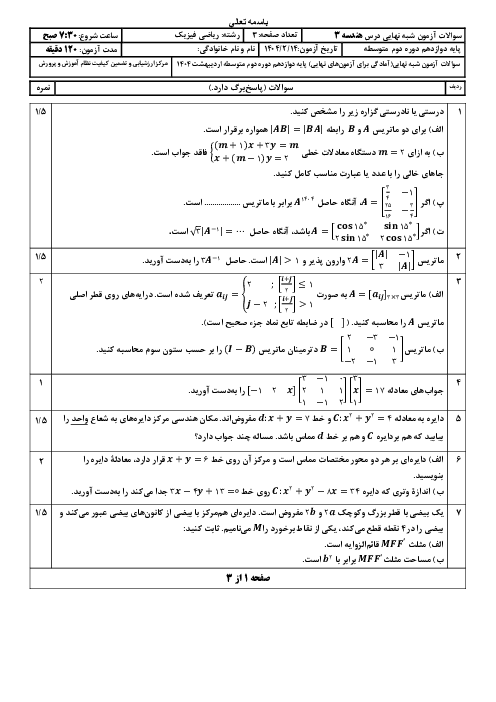
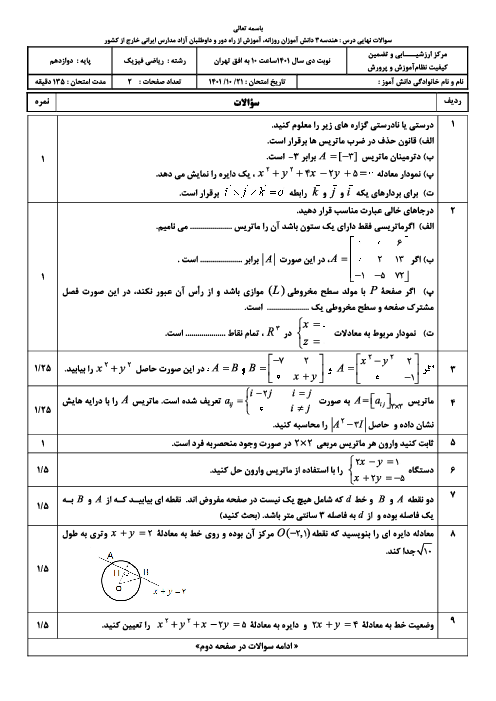
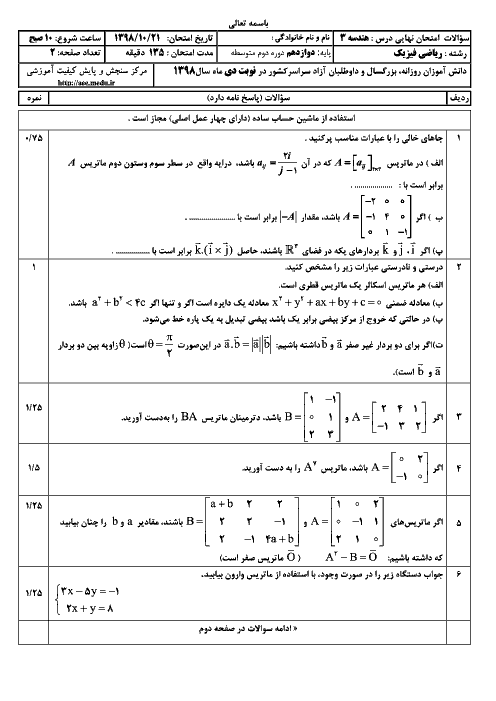
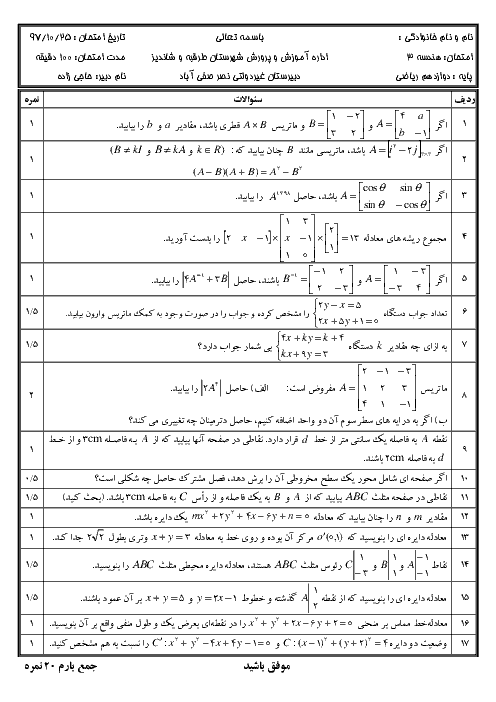
${{\left| \overrightarrow{a}-\overrightarrow{b} \right|}^{2}}+{{\left| \overrightarrow{b}-\overrightarrow{c} \right|}^{2}}+{{\left| \overrightarrow{c}-\overrightarrow{a} \right|}^{2}}=2\left( {{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}+{{\left| \overrightarrow{c} \right|}^{2}} \right)-2\left( \overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}.\overrightarrow{c}+\overrightarrow{a}.\overrightarrow{c} \right)=3$

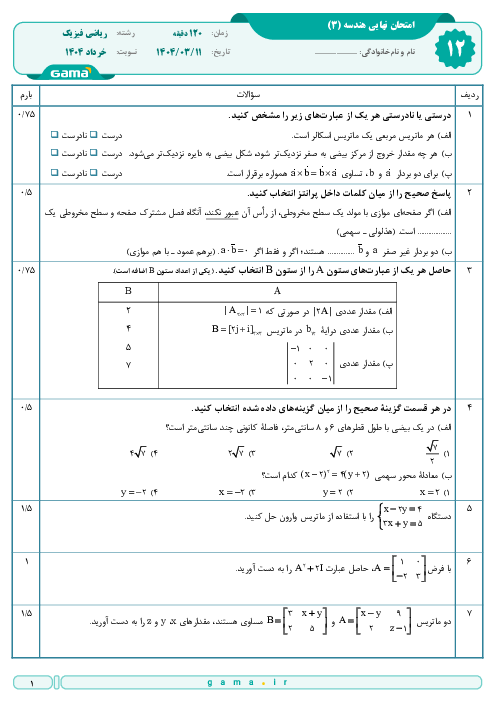
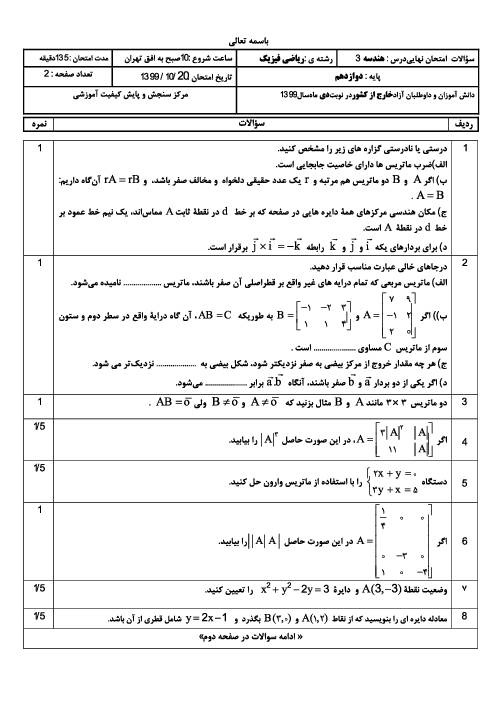
$\left( {{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}+{{\left| \overrightarrow{c} \right|}^{2}} \right)-{{\left| \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c} \right|}^{2}}\Rightarrow 9=3\times 3-{{\left| \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c} \right|}^{2}}\Rightarrow \left| \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c} \right|=0$

$\Rightarrow \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{o}\Rightarrow \overrightarrow{b}+\overrightarrow{c}=-\overrightarrow{a}$ 

$\left| 2\overrightarrow{a}+5\overrightarrow{b}+5\overrightarrow{c} \right|=\left| 2\overrightarrow{a}+5(\overrightarrow{b}+\overrightarrow{c}) \right|=\left| 2\overrightarrow{a}+5(-\overrightarrow{a}) \right|=\left| -3\overrightarrow{a} \right|=3\left| \overrightarrow{a} \right|=3$