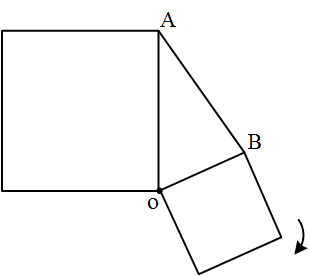
مانند شکل مقابل، دو مربع به مساحت‌های $x + 1$ و $x - 1$ داریم که در نقطهٔ O بهم متصل‌اند. می‌خواهیم مربع کوچک‌تر را حول نقطهٔ O چنان دوران دهیم که مساحت مثلث AoB بیشترین مقدار ممکن باشد. در این صورت مساحت مثلث AoB چقدر است؟
1 )
$\frac{{x - 1}}{2}$
2 )
$\frac{{x + 1}}{2}$
$\frac{{\sqrt {{x^2} - 1} }}{2}$
4 )
$\frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...