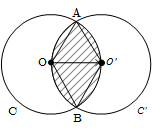
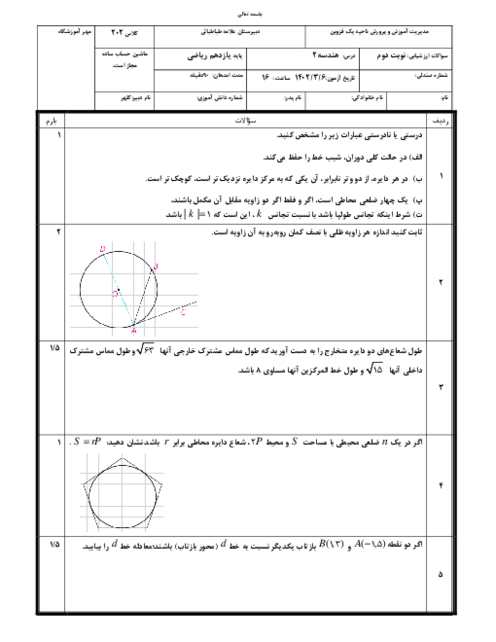
با توجه به شكل، چون اندازهٔ بردار $\overrightarrow{V}$ برابر شعاع دايره است، پس برای رسم انتقال يافتهٔ دايرهٔ $C$ تحت اين بردار،كافی است دايرهای به مرکز ${O}'$ و شعاع 1 رسم كنيم، بهطوری كه $\overrightarrow{O{O}'}=\overrightarrow{V}$. اکنون باید مساحت قسمت هاشور خورده را تعيين كنيم كه اين قسمت، از يک لوزی و چهار قطعه تشكيل شده است. پس داريم:
${{S}_{AOB{O}'}}=2{{S}_{O\overset{\Delta }{\mathop{A{O}'}}\,}}=2(\frac{\sqrt{3}}{4}O{{{O}'}^{2}})=\frac{\sqrt{3}}{2}$
${{S}_{O\overset{\Delta }{\mathop{A}}\,{O}'}}$ - مساحت قطاع ${{60}^{{}^\circ }}$ = مساحت یک قطعه
$=\frac{60}{360}(\pi \times {{1}^{2}})-(\frac{\sqrt{3}}{4}\times {{1}^{2}})=\frac{\pi }{6}-\frac{\sqrt{3}}{4}$
بنابراين مساحت خواسته شده برابر است با:
$\frac{\sqrt{3}}{2}+4(\frac{\pi }{6}-\frac{\sqrt{3}}{4})=\frac{2\pi }{3}-\frac{\sqrt{3}}{2}$