درس 1: مفهوم حد و فرآیندهای حدی
حسابان (1)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
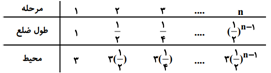
مطابق شكل، مثلثی متساوی‌الاضلاع داريم كه در هر مرحله، اوساط اضلاع آن را به هم متصل می‌كنيم تا مثلثی جديد تشكيل شود. در مرحلهٔ $n$ام اختلاف محيط مثلث رنگی ايجاد شده با عددی كه محيط‌های مثلث‌های رنگی به آن نزديک می‌شوند، كم‌تر از $\frac{1}{150}$ می‌شود، حداقل مقدار $n$ کدام است؟ (طول ضلع مثلث مرحلهٔ اول را واحد درنظر بگيريد.)
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...