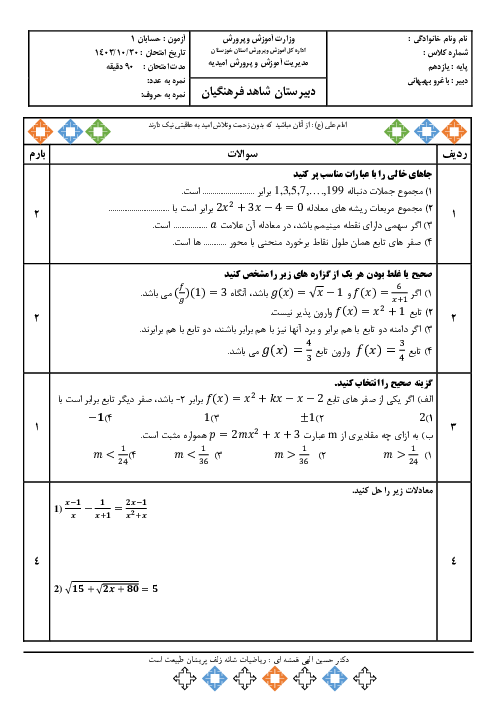
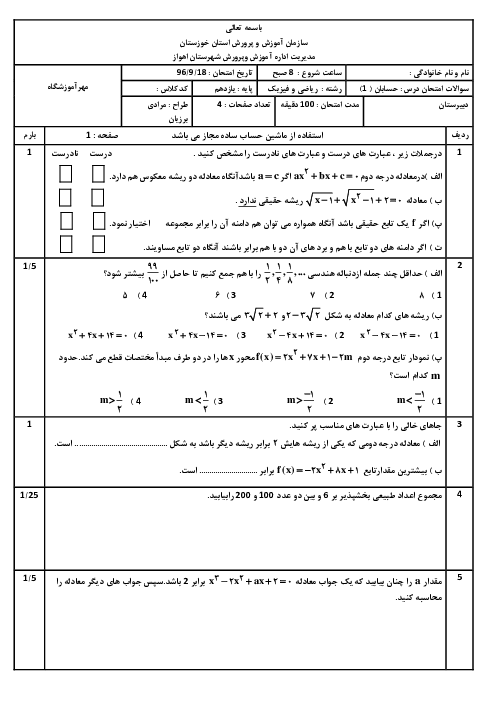
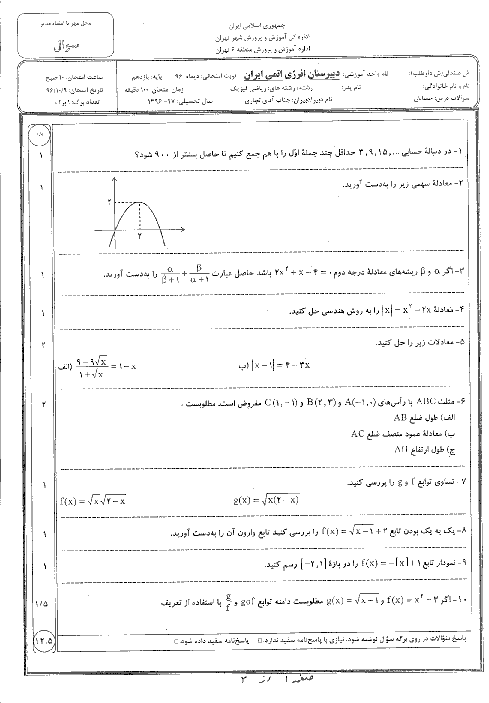
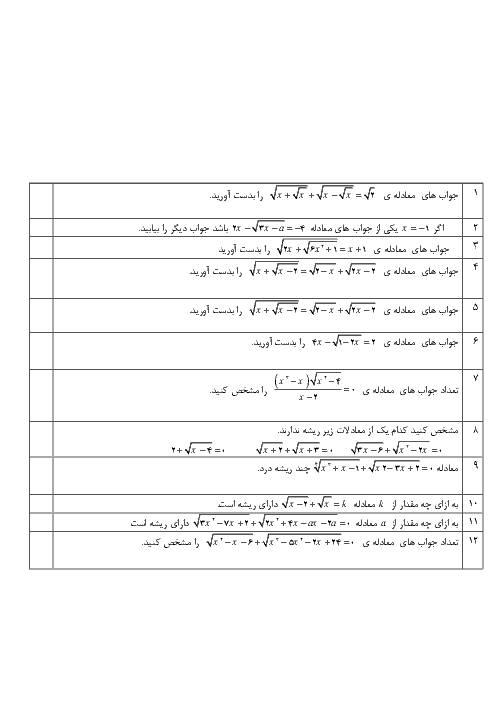
دو ضلع از مستطیلی روی خطهای $3x - 2y - 5 = 0$ و قرار $2x + 3y + 6 = 0$ دارند و نقطهٔ $( - 2,1)$ یک رأس این مستطیل است.
الف) مساحت این مستطیل را بیابید.
ب) معادلهٔ ضلع روبرو به خط $3x - 2y - 5 = 0$ در این مستطیل را بیابید.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!