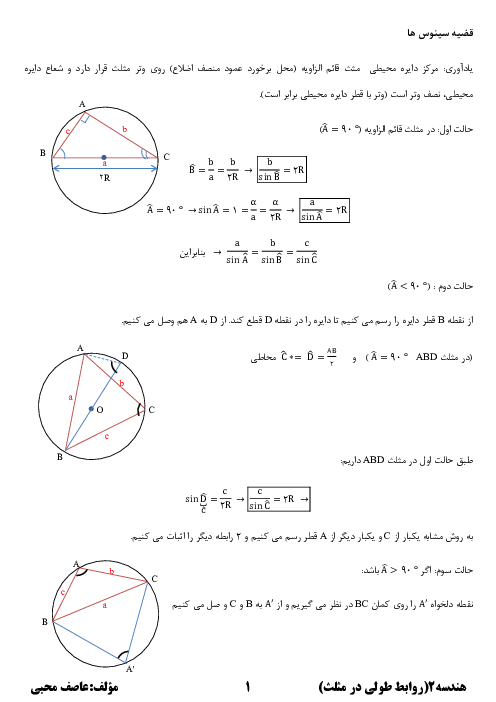
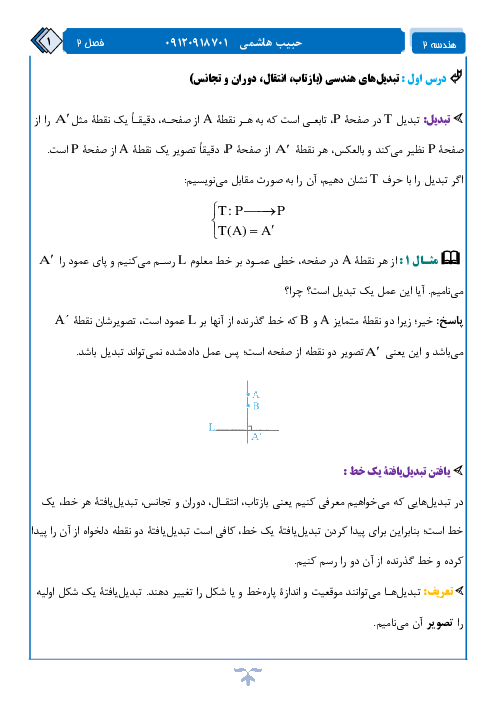
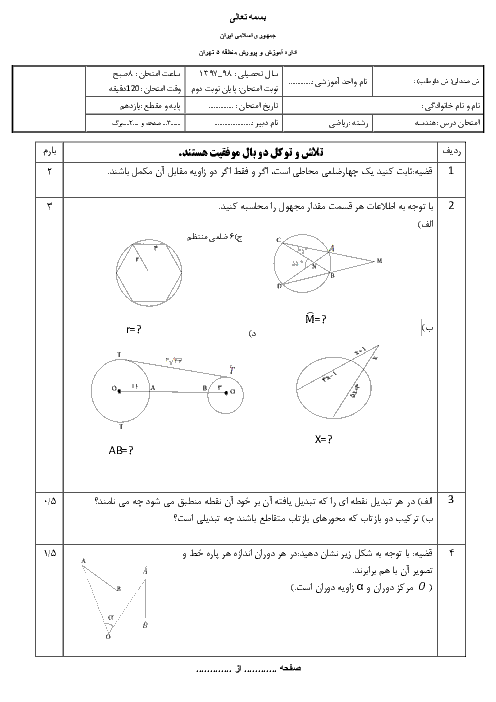
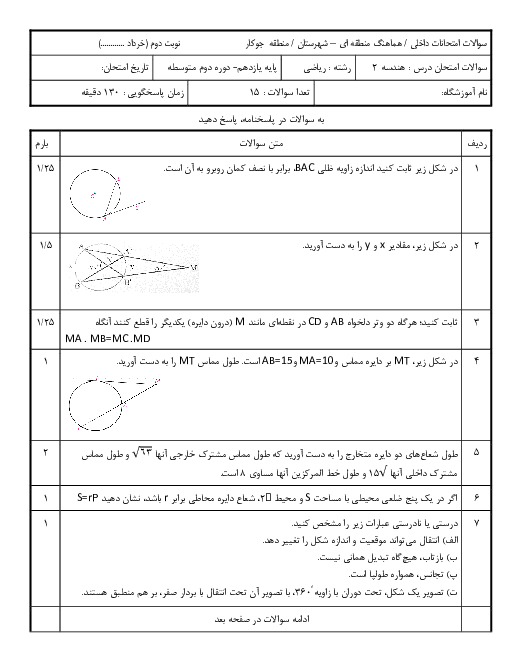
با توجه به رابطهٔ سينوس‌ها در مثلث داريم: 

$\frac{a}{\sin \hat{A}}=\frac{b}{\sin \hat{B}}\Rightarrow \frac{{{a}^{2}}}{{{b}^{2}}}=\frac{{{\sin }^{2}}\hat{A}}{{{\sin }^{2}}\hat{B}}$

$\frac{{{\sin }^{2}}\hat{A}}{{{\sin }^{2}}\hat{B}}=\frac{\tan \hat{A}}{\tan \hat{B}}\Rightarrow \frac{{{\sin }^{2}}\hat{A}}{{{\sin }^{2}}\hat{B}}=\frac{\frac{\sin \hat{A}}{\cos \hat{A}}}{\frac{\sin \hat{B}}{\cos \hat{B}}}\Rightarrow $

$\Rightarrow \frac{\sin \hat{A}}{\sin \hat{B}}=\frac{\cos \hat{B}}{\cos \hat{A}}\Rightarrow \sin \hat{A}\times \cos \hat{A}=\sin \hat{B}\times \cos \hat{B}$

$\Rightarrow \frac{\sin (2\hat{A})}{2}=\frac{\sin (2\hat{B})}{2}\Rightarrow \sin (2\hat{A})=\sin (2\hat{B})$

سينوس دو زاويه با هم برابر شده است. اين دو زاويه يا با هم برابرند يا مكمل يكديگرند، پس:

$\left\{ \begin{matrix} 2\hat{A}=2\hat{B}\Rightarrow \hat{A}=\hat{B}  \\ 2\hat{A}+2\hat{B}={{180}^{{}^\circ }}\Rightarrow \hat{A}+\hat{B}={{90}^{{}^\circ }}\Rightarrow \hat{C}={{90}^{{}^\circ }}  \\ \end{matrix} \right.$

پس مثلث $ABC$ يا متساوی‌الساقين است و يا اين‌كه در رأس $C$ قائم‌الزاویه $(\hat{C}={{90}^{{}^\circ }})$ می‌باشد.