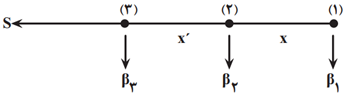
${{\beta }_{2}}-{{\beta }_{1}}=10\log \frac{{{I}_{2}}}{{{I}_{1}}}=10\log {{(\frac{{{r}_{1}}}{{{r}_{2}}})}^{2}}\Rightarrow 20=10\log {{(\frac{{{r}_{1}}}{{{r}_{2}}})}^{2}}$

$\Rightarrow 2=\log {{(\frac{{{r}_{1}}}{{{r}_{2}}})}^{2}}\Rightarrow {{10}^{2}}={{(\frac{{{r}_{1}}}{{{r}_{2}}})}^{2}}\Rightarrow \frac{{{r}_{1}}}{{{r}_{2}}}=10\Rightarrow {{r}_{1}}=10{{r}_{2}}$

${{\beta }_{3}}-{{\beta }_{2}}=10\log \frac{{{I}_{3}}}{{{I}_{2}}}=10\log {{(\frac{{{r}_{2}}}{{{r}_{3}}})}^{2}}\Rightarrow 20=10\log {{(\frac{{{r}_{2}}}{{{r}_{3}}})}^{2}}$

$\Rightarrow 2=\log {{(\frac{{{r}_{2}}}{{{r}_{3}}})}^{2}}\Rightarrow {{10}^{2}}={{(\frac{{{r}_{2}}}{{{r}_{3}}})}^{2}}\Rightarrow \frac{{{r}_{2}}}{{{r}_{3}}}=10\Rightarrow {{r}_{2}}=10{{r}_{3}}$

$\Rightarrow {{r}_{3}}=\frac{{{r}_{2}}}{10}$

$\Rightarrow {{r}_{1}}-{{r}_{2}}=x\Rightarrow 10{{r}_{2}}-{{r}_{2}}=x\Rightarrow x=9{{r}_{2}}$

$\Rightarrow {{r}_{2}}-{{r}_{3}}={x}'\Rightarrow {{r}_{2}}-\frac{{{r}_{2}}}{10}={x}'\Rightarrow {x}'=\frac{9}{10}{{r}_{2}}$

$\Rightarrow \frac{{{x}'}}{x}=\frac{\frac{9}{10}{{r}_{2}}}{9{{r}_{2}}}=\frac{1}{10}\Rightarrow {x}'=\frac{1}{10}x$