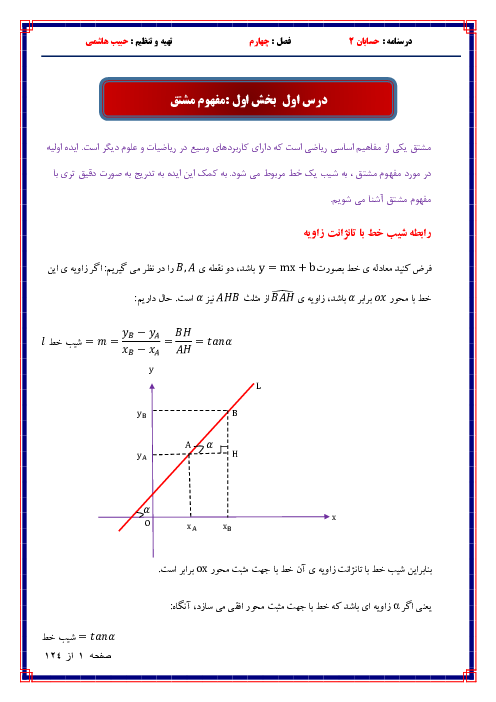
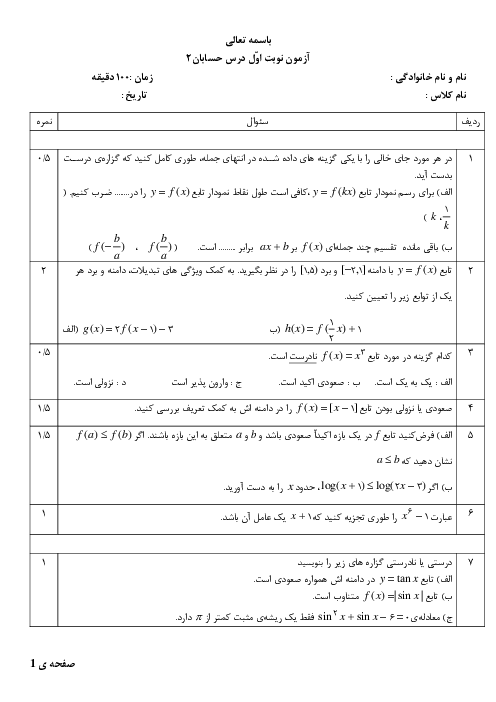
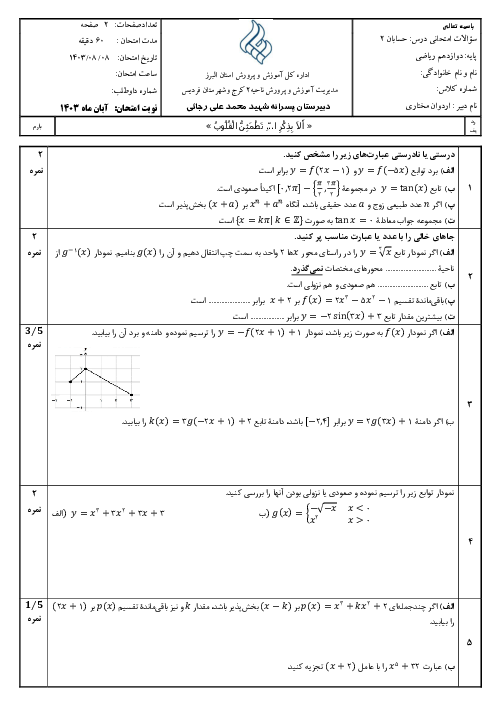
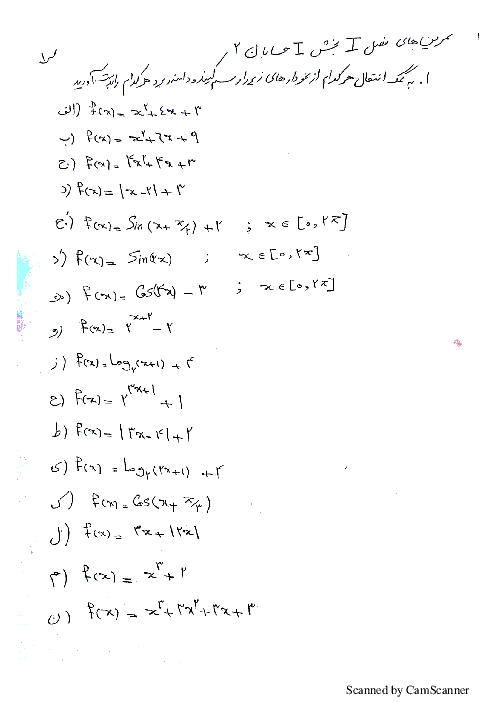باید $a \gt 0$ باشد، زیرا اگر $a \lt 0$ باشد، دامنه‌ی تابع، کران‌دار خواهد بود و $x$ نمی‌تواند به $\pm \infty $ میل کند. از طرفی در تابع $f(x)=2x-1+\sqrt{a{{x}^{2}}+bx}$ اگر $x\to +\infty $ آن‌گاه $f(x)\to +\infty $. بنابراین تابع در $-\infty $ مجانب افقی دارد.

$\underset{x\to -\infty }{\mathop{\lim }}\,f(x)=\underset{x\to -\infty }{\mathop{\lim }}\,(2x-1+\sqrt{a{{x}^{2}}+bx})\times \frac{(2x-1)-\sqrt{a{{x}^{2}}+bx}}{(2x-1)-\sqrt{a{{x}^{2}}+bx}}$

$=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{{{(2x-1)}^{2}}-(a{{x}^{2}}+bx)}{(2x-1)-\sqrt{a{{x}^{2}}+bx}}=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{(4-a){{x}^{2}}-(4+b)x+1}{(2x-1)-\sqrt{a}\left| x \right|\sqrt{1+\frac{b}{ax}}}=\frac{3}{2}$ 

باید ضریب ${{x}^{2}}$ صفر شود پس: $4-a=0\Rightarrow a=4$. داریم: 

$=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{-(4+b)x+1}{2x+\sqrt{4x}}=\frac{3}{2}\Rightarrow \frac{-4-b}{4}=\frac{3}{2}\Rightarrow -4-b=6\Rightarrow b=-10$