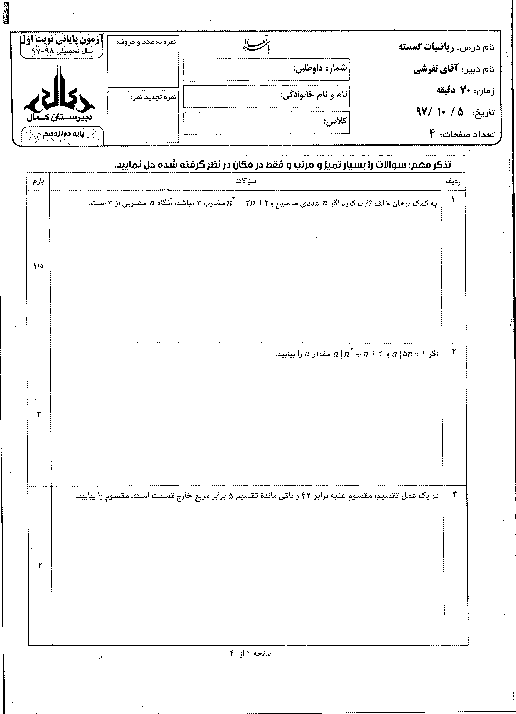
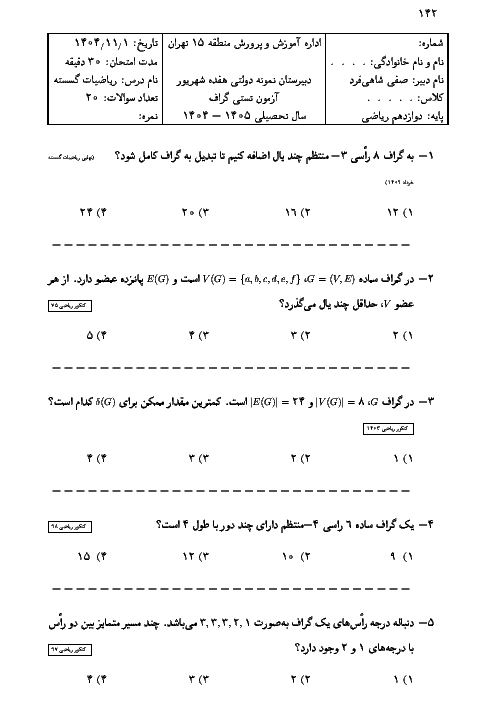
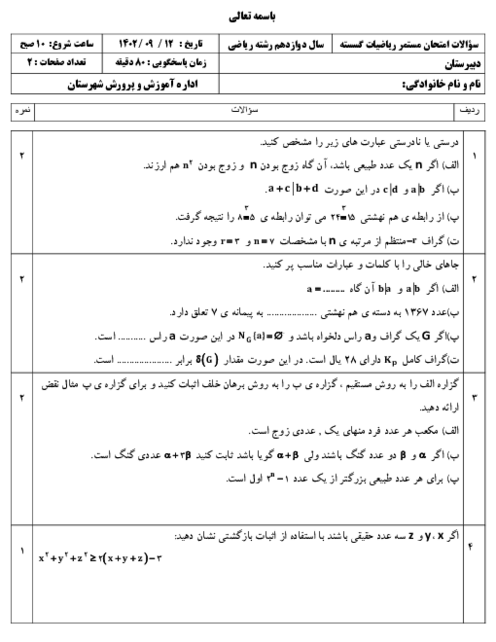
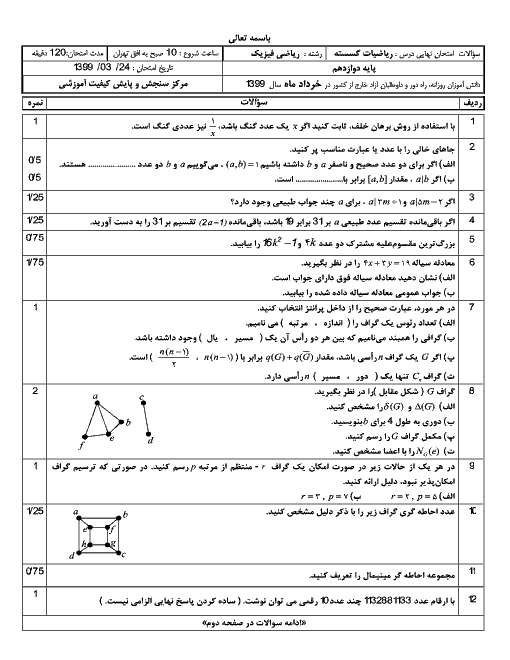
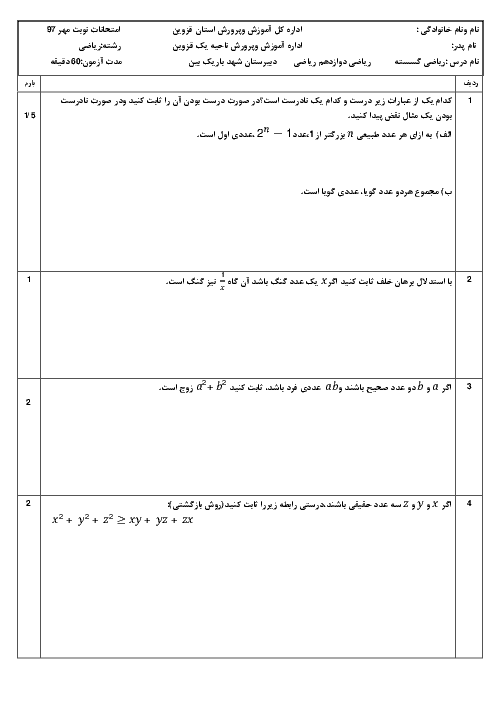
نکته: $ac\overset{m}{\mathop{\equiv }}\,bc\Rightarrow a\overset{\frac{m}{\left( m,c \right)}}{\mathop{\equiv }}\,b$

نکته: می‌توان به یک طرف یا هر دو طرف یک رابطۀ هم نهشتی، مضربی از پیمانه را اضافه کرد:

$ac\overset{m}{\mathop{\equiv }}\,b\Rightarrow a\overset{m}{\mathop{\equiv }}\,mk+b,a+mk\overset{m}{\mathop{\equiv }}\,b,a+mk\overset{m}{\mathop{\equiv }}\,b+m{k}'$

با استفاده از نکات بالا داریم:

$17a+29b=11\Rightarrow 17a+29b\overset{17}{\mathop{\equiv }}\,11$

$\Rightarrow 0+29b\overset{17}{\mathop{\equiv }}\,11\Rightarrow 12b\overset{17}{\mathop{\equiv }}\,11$

$\Rightarrow 12b\overset{17}{\mathop{\equiv }}\,\overbrace{11+17}^{28}\xrightarrow[\left( 4,17 \right)=1]{\div 4}3b\overset{17}{\mathop{\equiv }}\,7$ $\Rightarrow 3b\overset{17}{\mathop{\equiv }}\,\overbrace{7+17}^{24}\xrightarrow[\left( 3,17 \right)=1]{\div 3}b\overset{17}{\mathop{\equiv }}\,8$

بنابراین باقی‌ماندهٔ تقسیم عدد $b$ بر 17 برابر 8 است.