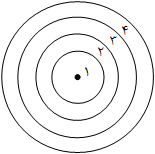
در تیراندازی به یک صفحهٔ دایره‌ای شکل که مطابق شکل زیر به چهار ناحیه‌ی مجزا تقسیم شده است، اگر احتمال اصابت به ناحیه‌ی kام، $(۳k-۲)x$ باشد، احتمال اصابت به ناحیه‌ی سوم چقدر است؟ (مرز بین دو ناحیه را جزء ناحیه‌ی کوچک‌تر محسوب کنید)
$\frac{۱}{۲۲}$
$\frac{۴}{۲۲}$
$\frac{۷}{۲۲}$
$\frac{۸}{۲۲}$
برای دیدن پاسخ تشریحی یک گزینه را انتخاب کن یا بزن رو