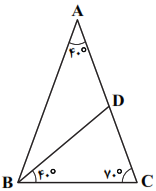
نكته: در هر مثلث، اندازه‌ی هر زاويه‌ی خارجی برابر مجموع اندازه‌های دو زاويه‌ی داخلی غيرمجاور آن است.

نكته: در هر مثلث با دو زاويه‌ی نابرابر، ضلع روبه‌رو به زاويه‌ی بزرگ‌تر، از ضلع روبه‌رو به زاويه‌ی كوچك‌تر، بزرگ‌تر است.

در مثلث BCD اندازه‌ی زاویه‌ی خارجی D برابر است با:

$B\hat{D}A={{40}^{{}^\circ }}+{{70}^{{}^\circ }}={{110}^{{}^\circ }}$

بنابراین:

$B\hat{D}C={{180}^{{}^\circ }}+{{110}^{{}^\circ }}={{70}^{{}^\circ }}$

پس مثلث BCD متساوی‌الساقین است و $BD=BC$

در مثلث ABD، زاویه‌ی خارجی D برابر ${{70}^{{}^\circ }}$ است، پس:

$B\hat{D}C={{40}^{{}^\circ }}+A\hat{B}D\Rightarrow A\hat{B}D={{30}^{{}^\circ }}$

بنابراین $\hat{B}=\hat{C}={{70}^{{}^\circ }}$، در نتیجه مثلث ABC نیز متساوی‌الساقین است و $AB=AC$ اکنون با استفاده از نکته‌ی بالا داریم:

$\begin{align}
  & \vartriangle ABD:A\hat{D}B\gt B\hat{A}D\Rightarrow AB\gt BD \\ 
 & \vartriangle BDC:D\hat{C}B\gt D\hat{B}C\Rightarrow BD\gt DC \\ 
\end{align}$

بنابراین گزینه‌ی 3 پاسخ است.