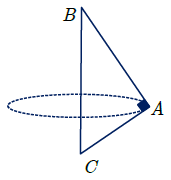
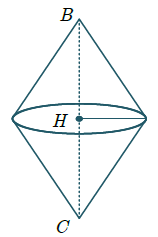
در واقع شکل حاصل به صورت دو مخروط هم قاعده که بهم چسبیدهاند یکی دارای ارتفاع CH و دیگری دارای ارتفاع BH است. (مطابق شکل زیر)
طبق رابطه فیثاغورس $B{C^2} = A{B^2} + A{C^2} \to BC = \sqrt {9 + 3} = \sqrt {12} - \sqrt {4 \times 2} = 2\sqrt 3 $
از طرفی $AH \times BC = AB \times AC \to AH = \frac{{AB \times AC}}{{BC}} \Rightarrow AH = \frac{{3 \times \sqrt 3 }}{{2\sqrt 3 }} = \frac{3}{2}$
پس هر دو مخروط دارای قاعدهای به شعاع $\frac{3}{2}$ است.
شکل $V = {V_1} + {V_2} = \frac{1}{3}S \times BH + \frac{1}{3}S \times CH \to $ در مخروط همقاعده هستند $\frac{1}{3}S\underbrace {(BH + CH)}_{BC}$
$ = \frac{1}{3}S \times BC = \frac{1}{3}\left( {{{(\frac{3}{2})}^2} \times \pi } \right) \times 2\sqrt 3 = \frac{3}{2}\sqrt 3 \pi $