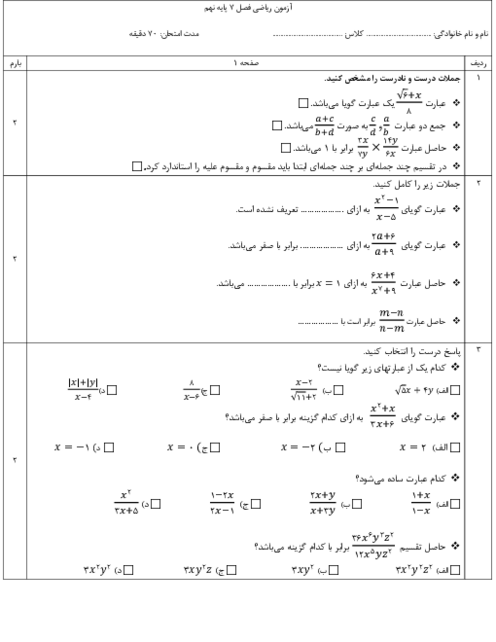
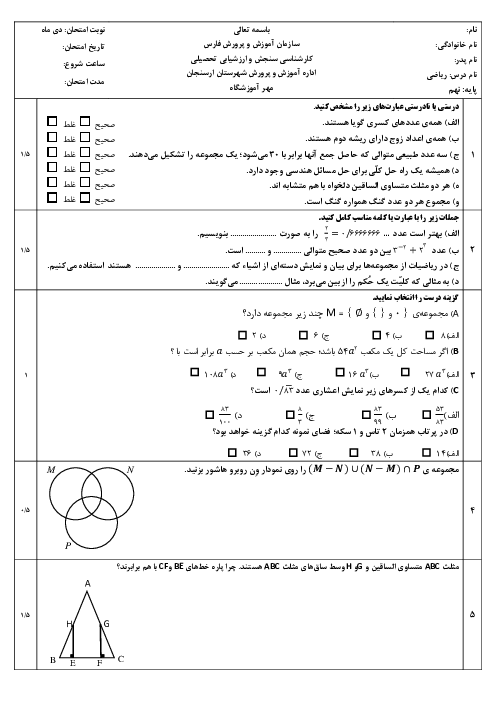
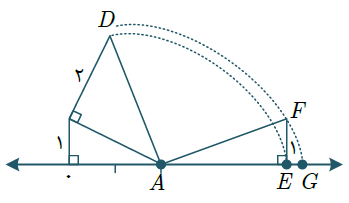
در شکل مقابل به مرکز A و به شعاع AD کمانی زدهایم تا محور را در E قطع کند، سپس به مرکز A و به شعاع AF کمانی میزنیم تا محور را در G قطع کند، طول پارهخط EG چقدر است؟
2 )
$2 - \sqrt {10} $3 )
$3 - \sqrt {10} $4 )
$ - 2 + \sqrt {10} $پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!