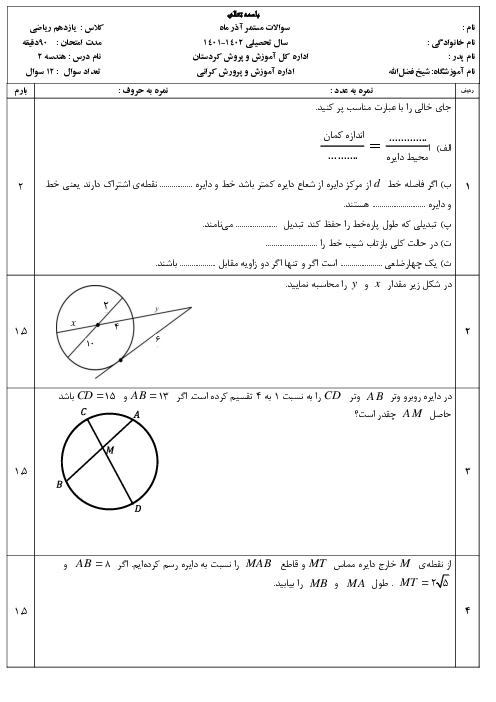
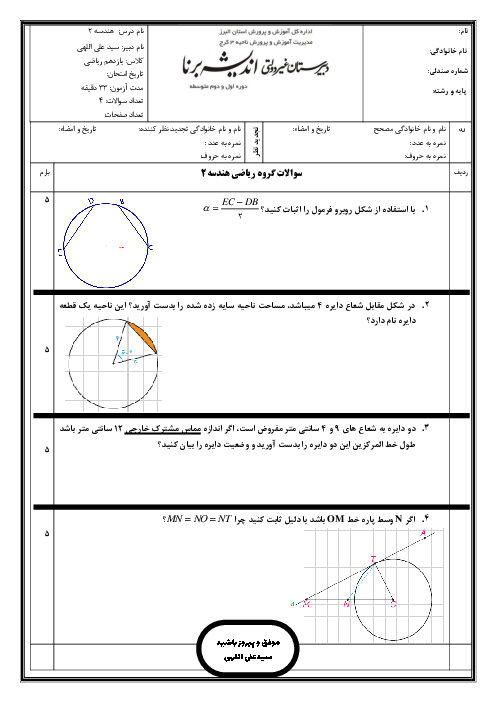
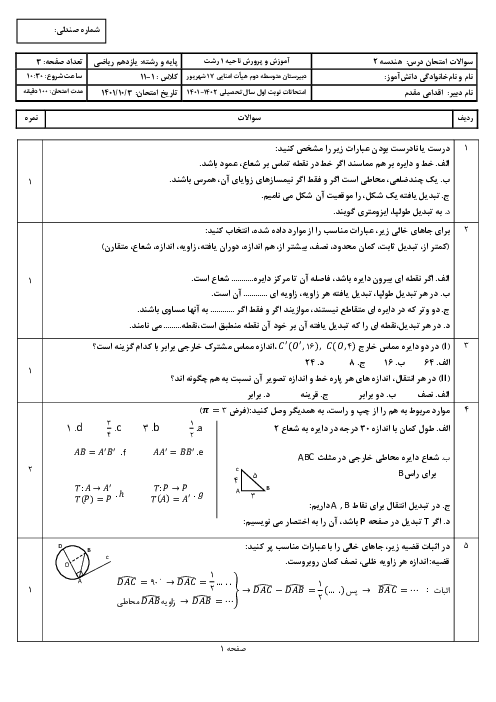
درس 4: قضیۀ هرون (محاسبۀ ارتفاعها و مساحت مثلث)
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
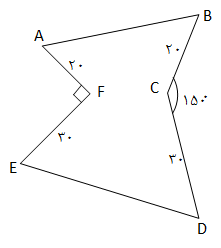
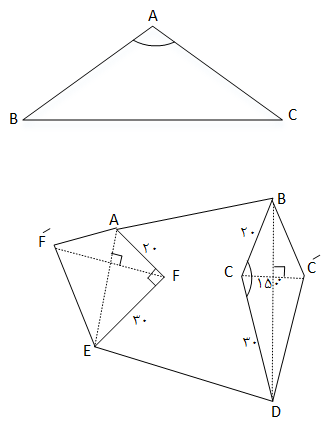
در شكل مقابل اگر بدون تغيير محيط و تعداد اضلاع، مساحت شكل را به كمک بازتاب افزايش دهيم، ميزان افزايش مساحت كدام است؟