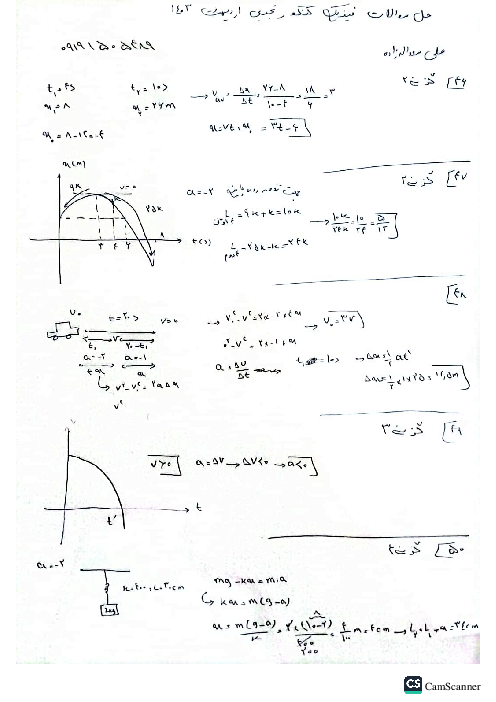
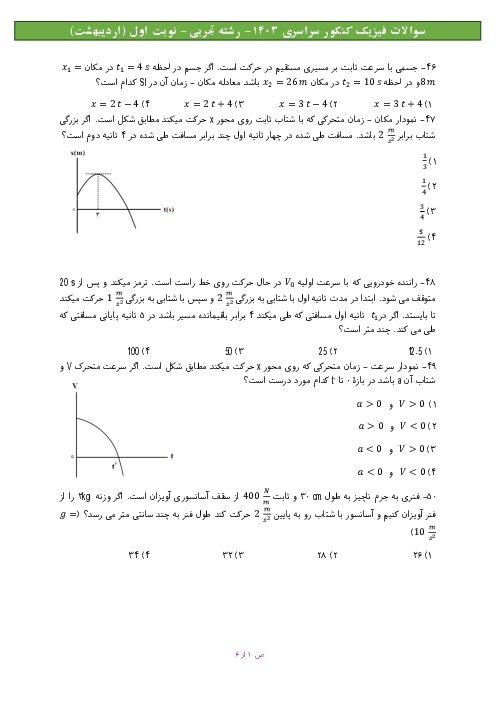
گام اول: در حرکت با شتاب ثابت، سرعت در لحظهٔ وسط یک بازهٔ زمانی برابر سرعت متوسط در همان بازه است. پس در اینجا سرعت در لحظهٔ وسط $(1s,6s)$ برابر سرعت متوسط این بازه یعنی $3m/s$ است:

${{V}_{av(1,6)}}=3m/s\xrightarrow{t=\frac{1+6}{2}=3/5s}{{V}_{3/5}}=3m/s$

گام دوم: با توجه به نمودار، سرعت در لحظهٔ $t=2s$ برابر صفر است، پس با داشتن سرعت در لحظه‌های $t=2s$ و ${t}'=3/5s$ می‌توانیم شتاب را حساب کنیم:

$a=\frac{\Delta v}{\Delta t}=\frac{{{v}_{3/5}}-{{v}_{2}}}{3/5-2}=\frac{3-0}{1/5}=2m/{{s}^{2}}$

گام سوم: روش 1 در لحظهٔ $t=2s$ متحرک تغییر جهت داده است. پس برای این‌ که مسافت طی‌شده توسط متحرک در مدت $1s$ تا $6s$ را به دست بیاوریم، باید اندازهٔ جابجایی‌های متحرک در بازهٔ $(1s,2s)$ و $(2s,6s)$ را با هم جمع کنیم. برای این کار می‌توانیم به جای جابجایی $1s$ تا $2s$، جابجایی $2s$ تا $3s$ را حساب کنیم (چون قرینه‌اند).

$\left\{ \begin{matrix} \left| \Delta {{x}_{(1,2)}} \right|=\Delta {{x}_{(2,3)}}=\frac{1}{2}a{{(\Delta {{t}_{(2,3)}})}^{2}}+{{v}_{2}}\Delta {{t}_{(2,3)}} \\ \xrightarrow[\Delta {{t}_{(2,3)}}]{{{v}_{2}}=0}\Delta {{x}_{(2,3)}}=\frac{1}{2}\times 2\times {{1}^{2}}+0=1m \\ \Delta {{x}_{(2,6)}}=\frac{1}{2}a{{(\Delta {{t}_{(2,6)}})}^{2}}+{{v}_{2}}\Delta {{t}_{(2,6)}} \\ \xrightarrow{\Delta {{t}_{(2,6)=4s}}}\Delta {{x}_{(2,6)}}=\frac{1}{2}\times 2\times {{4}^{2}}+0=16m \\ \end{matrix} \right.$

$\Rightarrow {{\ell }_{(1,6)}}=\left| \Delta {{x}_{(1,2)}} \right|+\Delta {{x}_{(2,6)}}=1+16=17m$

روش 2 گام سوم را می‌توانید با رسم نمودار سرعت ـ زمان هم حساب کنید.