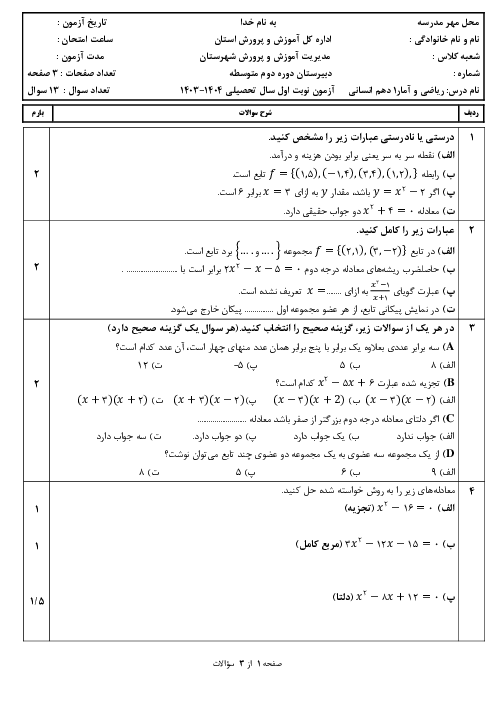
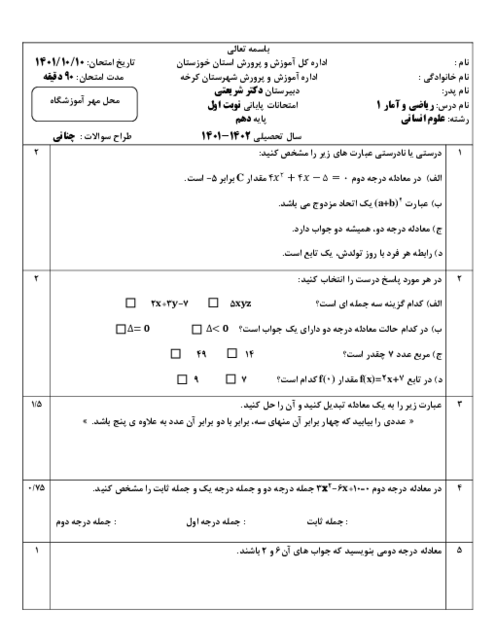
درس 4: رسم تابع درجۀ 2
ریاضی و آمار (1)
دهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
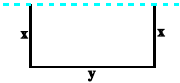
میخواهیم با یک قطعه سیم به طول 56 متر، زمینی به شکل مستطیل که یک طرف آن دیوار است، محصور شود. بیشترین مساحت زمین محصور شده، کدام است؟

تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!