درس 2: حل معادلۀ درجۀ 2 و کاربردها
ریاضی و آمار (1)
دهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
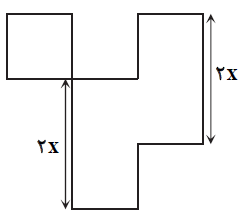
در شکل روبهرو، اندازهٔ تمام پارهخطها به جز دو پاره خط مشخص شده، برابر x است. اگر اندازهٔ مساحت شکل برابر محیط شکل باشد، مقدار x کدام است؟