$HA$ یک اسید ضعیف تک عاملی است، بنابراین رابطهٔ $\left[ {{H}^{+}} \right]=\sqrt{{{K}_{a}}\times M}$ برای آن قابل استفاده است.

$\left[ {{H}^{+}} \right]=\sqrt{{{K}_{a}}\times M}=\sqrt{2\times {{10}^{-8}}\times {{M}_{HA}}}$

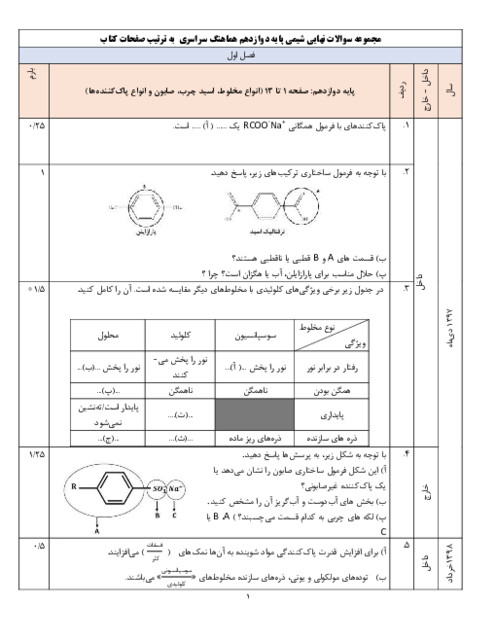
$\left[ {{H}^{+}} \right]\left[ O{{H}^{-}} \right]={{10}^{-14}}\Rightarrow \left[ O{{H}^{-}} \right]=\frac{{{10}^{-14}}}{\left[ {{H}^{+}} \right]}=\frac{{{10}^{-14}}}{\sqrt{2\times {{10}^{-8}}\times {{M}_{HA}}}}$

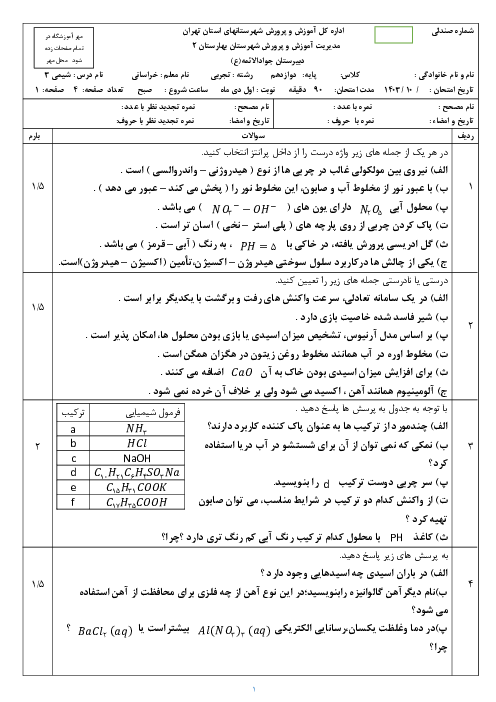
$BOH$ یک باز ضعیف تک عاملی است و می‌توان از رابطه $\left[ O{{H}^{-}} \right]=\sqrt{{{K}_{b}}\times M}$ استفاده کرد:

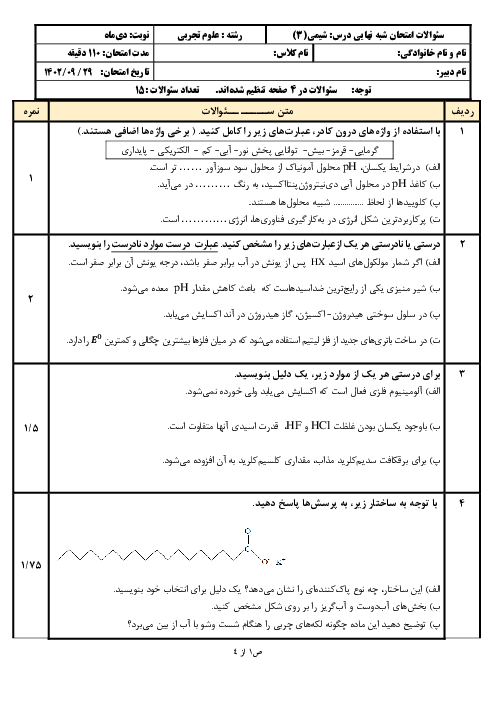
$\left[ O{{H}^{-}} \right]=\sqrt{{{K}_{b}}\times M}=\sqrt{4\times {{10}^{-10}}\times {{M}_{BOH}}}$

$\left[ {{H}^{+}} \right]\left[ O{{H}^{-}} \right]={{10}^{-14}}\Rightarrow \left[ {{H}^{+}} \right]=\frac{{{10}^{-14}}}{\left[ O{{H}^{-}} \right]}=\frac{{{10}^{-14}}}{\sqrt{4\times {{10}^{-10}}\times {{M}_{BOH}}}}$

$\frac{HA\left[ O{{H}^{-}} \right]}{BOH\left[ {{H}^{+}} \right]}=\frac{\frac{{{10}^{-14}}}{\sqrt{2\times {{10}^{-8}}\times {{M}_{HA}}}}}{\frac{{{10}^{-14}}}{\sqrt{4\times {{10}^{-10}}\times {{M}_{BOH}}}}}=\sqrt{\frac{4\times {{10}^{-10}}}{2\times {{10}^{-8}}}\times \frac{{{M}_{BOH}}}{{{M}_{HA}}}}=\sqrt{\frac{4\times {{10}^{-10}}}{2\times {{10}^{-8}}}\times 2}=0/2$