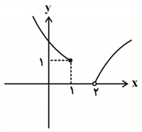
در تابع $f(x)=\left\{ \begin{matrix} \sqrt{x-2},x\gt 2 \\ {{(x-1)}^{2}}+1,x\le 1 \\ \end{matrix} \right.$، حاصل $\underset{x\to 1}{\mathop{\lim }}\,f(x)$ و $\underset{x\to 2}{\mathop{\lim }}\,f(x)$ به‌ترتيب از راست به چپ كدام است؟
1 )
1، صفر
2 )
وجود ندارد، صفر
3 )
1، وجود ندارد
وجود ندارد، وجود ندارد
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...