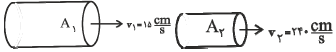چون آهنگ شارش آب در ورودی و خروجی شیلنگ با هم برابر است، با استفاده از معادله‌ی پیوستگی و با توجه به این که سطح مقطع شیلنگ دایره‌ای است و مساحت دایره برابر با $A=\pi {{r}^{2}}$ می‌باشد، به صورت زیر درصد تغییر شعاع شیلنگ را به دست می‌آوریم. آهنگ شارش آب ثابت است، در جایی که تندی آب بیش‌تر است، سطح مقطع لوله کوچک‌تر می‌باشد.

${{A}_{2}}{{v}_{2}}={{A}_{1}}{{v}_{1}}\xrightarrow{A=\pi {{r}^{2}}}\pi {{r}_{2}}^{2}\times {{v}_{2}}=\pi {{r}_{1}}^{2}\times {{v}_{1}}\Rightarrow$
$ \frac{{{r}_{2}}^{2}}{{{r}_{1}}^{2}}=\frac{{{v}_{1}}}{{{v}_{2}}} \Rightarrow$
$ {{(\frac{{{r}_{2}}}{{{r}_{1}}})}^{2}}=\frac{1}{16}\Rightarrow \frac{{{r}_{2}}}{{{r}_{1}}}=\frac{1}{4}\Rightarrow {{r}_{2}}=\frac{1}{4}{{r}_{1}}\Rightarrow \Delta r={{r}_{2}}-{{r}_{1}}=\frac{1}{4}{{r}_{1}}-{{r}_{1}}\Rightarrow$
$ \Delta r=-\frac{3}{4}{{r}_{1}}=-0/75{{r}_{1}}\Rightarrow \frac{\Delta r}{{{r}_{1}}}\times 100=-0{\scriptstyle{}^{0}/{}_{0}}75$ 

بنابراین باید شعاع شیلنگ، 75 درصد کاهش یابد.