معادله‌ی چند ریشه‌ی حقیقی دارد؟ | ریاضی (2) یازدهم شماره 64965

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

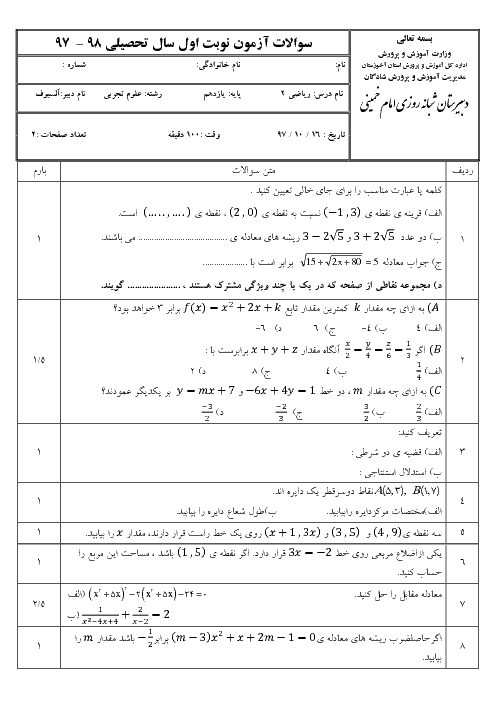
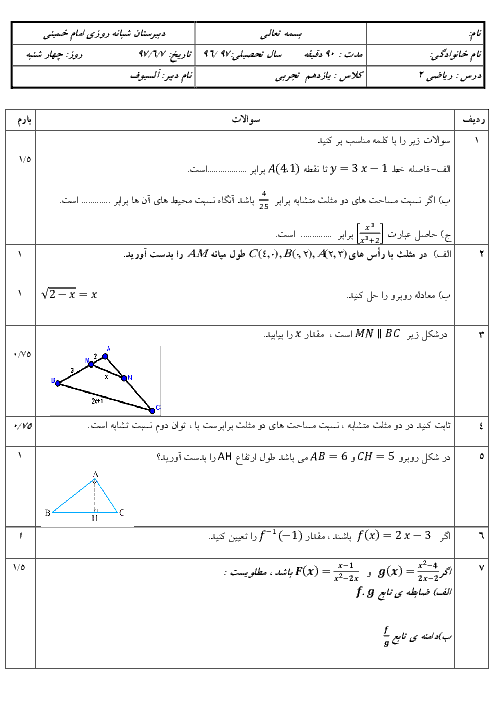
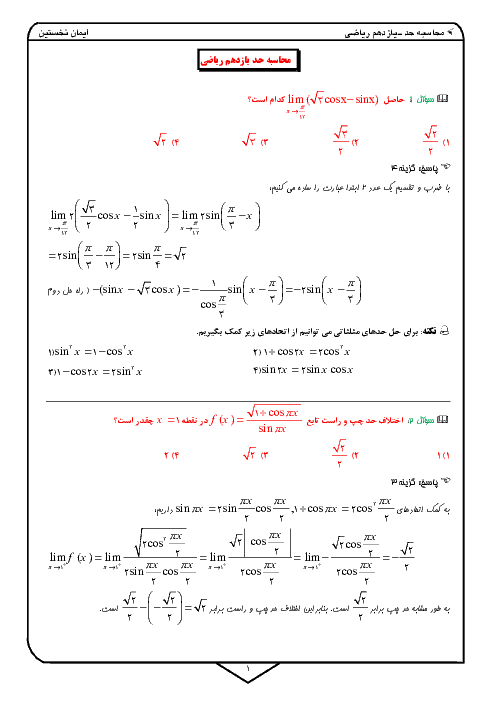
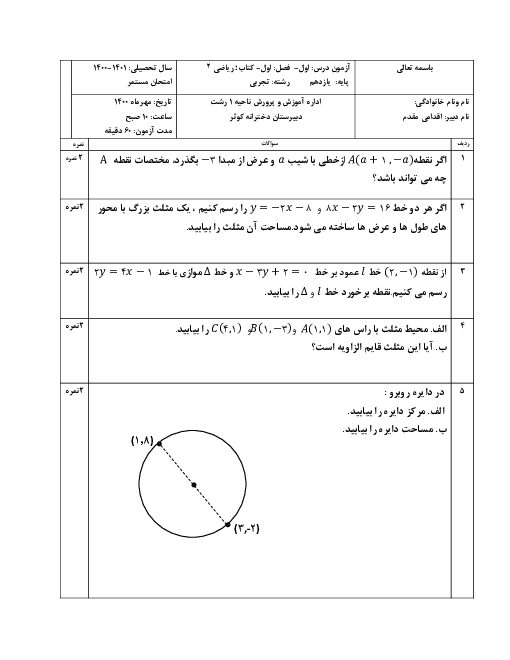
درس 3: معادلات گویا و معادلات رادیکالی ریاضی (2) یازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

معادله‌ی $\frac{1}{5+\sqrt{x}}+\frac{1}{5-\sqrt{x}}=\frac{10}{{{x}^{2}}+5}$ چند ریشه‌ی حقیقی دارد؟

1 )

2 )

3 )

صفر

4 )

نمایش پاسخ

نكته: برای حل يک معادله‌ی گويا ابتدا با مخرج مشترک گيری، عبارت را ساده ‌تر می‌كنيم. سپس معادله‌ی حاصل را حل می‌نماييم. در پايان قابل قبول بودن جواب‌های به ‌دست آمده را بررسی می‌كنيم.

ابتدا با شرط $x\ge 0$ ، طرف چپ معادله را ساده می‌كنيم:

$\frac{1}{5+\sqrt{x}}+\frac{1}{5-\sqrt{x}}=\frac{5-\sqrt{x}+5+\sqrt{x}}{(5+\sqrt{x})(5-\sqrt{x})}=\frac{10}{25-x}$

با جای‌ گذاری اين مقدار در معادله داريم:

$\frac{10}{25-x}=\frac{10}{{{x}^{2}}+5}\Rightarrow 25-x={{x}^{2}}+5\Rightarrow {{x}^{2}}+x-20=0\Rightarrow (x-4)(x+5)=0\Rightarrow \left\{ _{x=-5}^{x=4} \right.$

$x=-5$ در معادله‌ی اصلی صدق نمی‌كند، پس فقط $x=4$ قابل قبول است. بنابراين معادله‌ی موردنظر فقط يک ريشه دارد.

گزارش اشکال