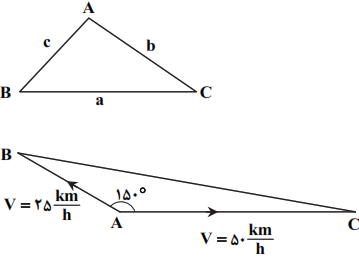
نكته (قضيه‌ی كسينوس‌ها): در مثلث دلخواه ABC داریم:

$\left\{ \begin{matrix}
   {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\operatorname{Cos}\hat{A}  \\
   {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\operatorname{Cos}\hat{B}  \\
   {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\operatorname{Cos}\hat{C}  \\
\end{matrix} \right.$

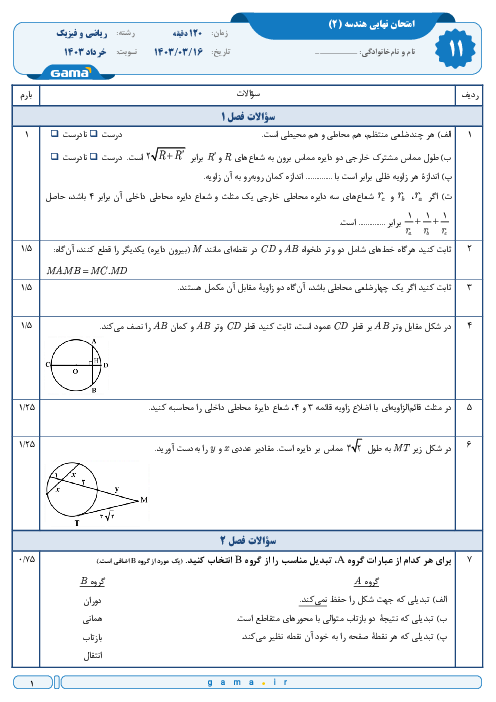
ابتدا به‌کمک رابطه‌ی $x=vt$ در حرکت با سرعت ثابت، مطابق شکل، داریم:

$\begin{align}
  & AB=25\times 2=50km \\ 
 & AC=50\times 2=100km \\ 
\end{align}$

و اینک با توجه به نکته، خواهیم داشت:

$\begin{align}
  & B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2(AB)(AC)\operatorname{Cos}{{150}^{{}^\circ }}=2500+10000-2(50)(100)(-0/85) \\ 
 & \Rightarrow B{{C}^{2}}=12500+8500=21000\Rightarrow BC=\sqrt{21000}=10\sqrt{210} \\ 
\end{align}$

بنابراین گزینه‌ی 2 پاسخ است.