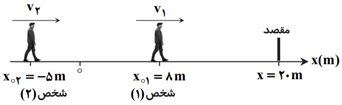
$\left\{ \begin{matrix} {{x}_{1}}={{v}_{1}}t+{{x}_{{}^\circ 1}}  \\ {{x}_{2}}={{v}_{2}}{t}'+{{x}_{{}^\circ 2}}  \\ \end{matrix}\Rightarrow \left\{ \begin{matrix} 20={{v}_{1}}t+8\Rightarrow t=\frac{12}{{{v}_{1}}},(1)  \\ 20=({{v}_{1}}+3)(t-1)-5,(2)  \\ \end{matrix} \right. \right.$

$(1),(2)\Rightarrow 20=({{v}_{1}}+3)(\frac{12}{{{v}_{1}}}-1)-5\Rightarrow v_{1}^{2}+16{{v}_{1}}-36=0$

${{v}_{1}}=\frac{-8\pm \sqrt{64+36}}{1}=-8\pm 10\Rightarrow \left\{ \begin{matrix} 2\frac{m}{s}  \\ -18\frac{m}{s}  \\ \end{matrix} \right.$

چون جهت حركت شخص (۱) در جهت مثبت محور $x$ است، ${{v}_{1}}=-18\frac{m}{s}$ قابل قبول نیست.