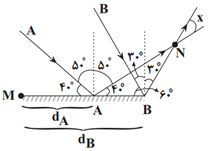
دو پرتو $A$ و $B$ به‌ترتیب با زاویه‌های تابش ${{50}^{{}^\circ }}$ و ${{30}^{{}^\circ }}$ به سطح آینه‌ای تخت برخورد می‌کنند و پس از بازتاب، پرتوهای بازتاب یکدیگر را در نقطهٔ $N$ قطع می‌کنند. اگر ${{d}_{A}}$ و ${{d}_{B}}$ به‌ترتیب فاصلهٔ نقطهٔ برخورد پرتوهای $A$ و $B$ با سطح آینه از انتهای آینه (نقطهٔ $M$) باشد، کدام گزینه در مورد زاویهٔ برخورد پرتوهای بازتاب ${{d}_{A}}$ و ${{d}_{B}}$ صحیح است؟
1 )
${{d}_{A}}\gt {{d}_{B}}$ و ${{60}^{{}^\circ }}$
2 )
${{d}_{A}}\lt {{d}_{B}}$ و ${{60}^{{}^\circ }}$
3 )
${{d}_{A}}\gt {{d}_{B}}$ و ${{20}^{{}^\circ }}$
${{d}_{A}}\lt {{d}_{B}}$ و ${{20}^{{}^\circ }}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...