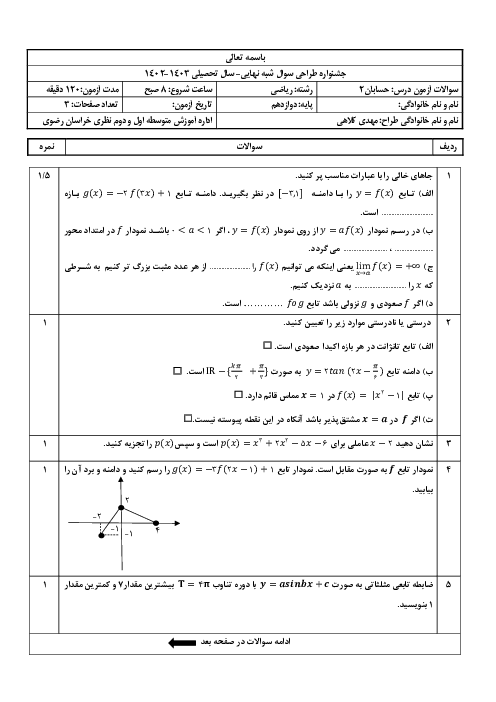
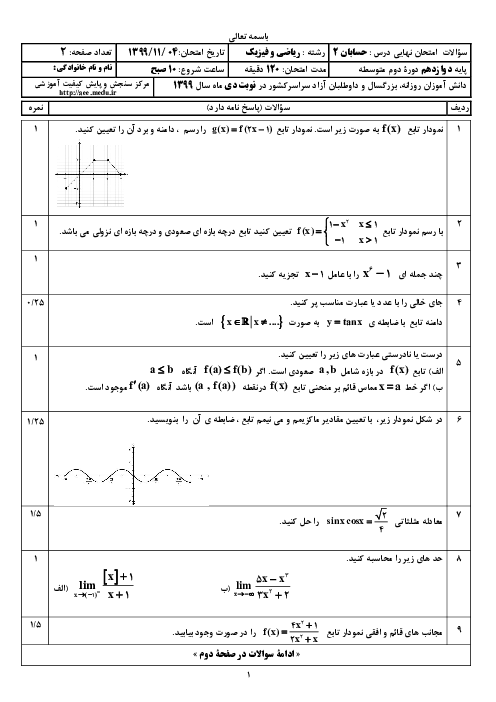
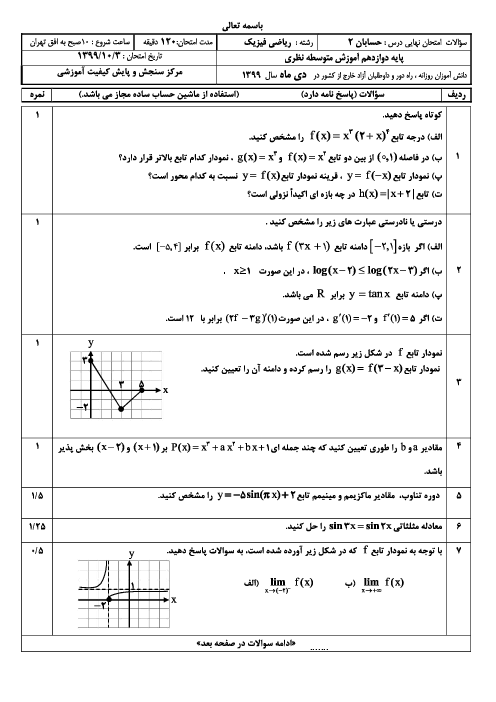
زوج مرتب $(b,a)$ کدام باشد تا تابع $f(x)=\left\{ \begin{matrix} a{{x}^{2}}+2bx+2\,\,\,\,\,;\,\,\,\,\,\left| x \right| \gt 1 \\ 4b+a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;\,\,\,\,\,\left| x \right|=1 \\ b- a{{x}^{3}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,;\,\,\,\,\,\left| x \right| \lt 1 \\ \end{matrix} \right.$ در $R$ مشتق‌پذیر باشد؟
1 )
$(1,-1)$
2 )
$(-1,1)$
3 )
$(\frac{1}{3},1)$
چنین $a$ و $b$ ای وجود ندارد.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...