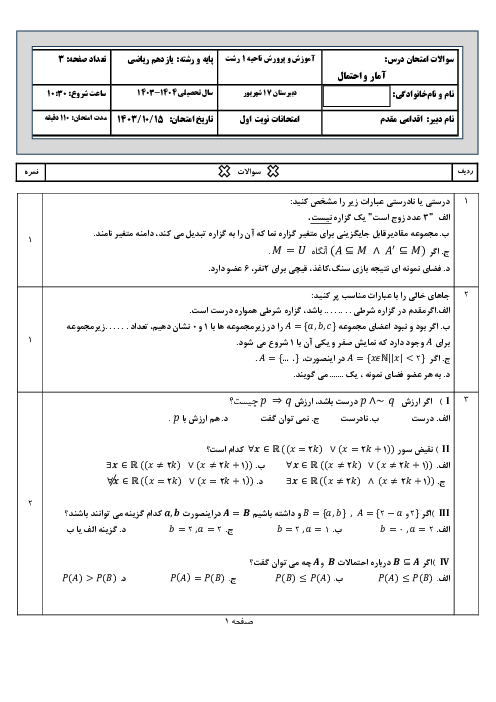
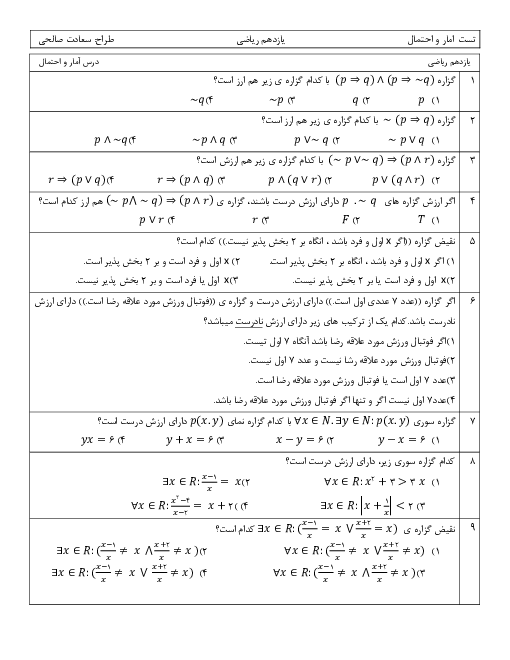
نکته‌ی 1: A و B دو پیشامد مستقل هستند اگر و فقط اگر:

$\begin{align}
  & 1)\,P(A\cap B)=P(A)\times P(B) \\ 
 & 2)\,P(A\left| B \right.)=P(A) \\ 
 & 3)\,P(B\left| A \right.)=P(B) \\ 
\end{align}$

نکته‌ی 2: اگر A و B دو پیشامد مستقل باشند آنگاه هر کدام از پیشامدهای «A و ${B}'$»، «B و ${A}'$» و «${A}'$ و ${B}'$» نیز مستقل هستند.

نکته 3 $:P({A}')=1-P(A)$
نکته 4 $:P(A\cup B)=P(A)+P(B)-P(A\cap B)$

با توجه به نکات داریم:

$P(A\left| {{B}'} \right.)=P(A)\Rightarrow {B}'\,,\,A$ مستقل‌اند

حال از آن‌جایی‌که A و ${B}'$ مستقل‌اند با توجه به نکته‌ی 2 واضح است که B و ${A}'$ نیز مستقل‌اند، پس با توجه به نکته‌ی 1، داریم:

$P(B\left| {{A}'} \right.)=P(B)=\frac{1}{4}$

و در نهایت با توجه به نکات 1،‌2 و 3 خواهیم داشت:

$\begin{align}
  & P(A\cup {B}')=P(A)+P({B}')-P(A\cap {B}')=\frac{2}{3}+1-P(B)-P(A)\times P({B}') \\ 
 & =\frac{2}{3}+1-\frac{1}{4}-\frac{2}{3}\times (1-\frac{1}{4})=\frac{2}{3}+\frac{3}{4}-\frac{1}{2}=\frac{11}{12} \\ 
\end{align}$

بنابراین گزینه‌ی 3 پاسخ است.