** فصل 1: الکتریسیتۀ ساکن
فیزیک (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
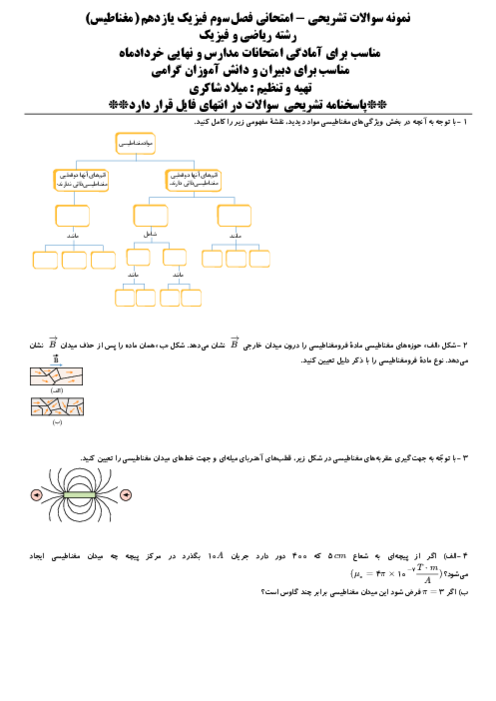
مطابق شکل، بارهای نقطه‌ای ${{q}_{1}}=10nC$ و ${{q}_{2}}$ در نقاط $A$ و $B$ قرار دارند و وقتی بار ${{q}_{3}}=20nC$ در نقطهٔ $C$ قرار بگیرد، برایند نیروهای وارد بر آن صفر می‌شود. اگر ${{q}_{1}}$ را خنثی کنیم و بار $2{{q}_{3}}$ در $C$ و $-3{{q}_{2}}$ در $B$ باشد، اندازهٔ نیروی الکتریکی که این دو بار بر یکدیگر وارد می‌کنند. چند نیوتون خواهد بود؟ $(k=9\times {{10}^{9}}\frac{N.{{m}^{2}}}{{{C}^{2}}})$
$1/2\times {{10}^{-4}}$
2 )
$1/8\times {{10}^{-4}}$
3 )
$2/4\times {{10}^{-3}}$
4 )
$3/6\times {{10}^{-3}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...