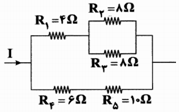
ابتدا باید جریان عبوری از هر مقاومت را محاسبه کرده و سپس با توجه به رابطه‌ی $Q=R{{I}^{2}}t$ گرمای تولیدشده در هر مقاومت را با یک‌دیگر مقایسه می‌کنیم:

$I={{I}_{1}}+{{I}_{2}}\xrightarrow{{{R}_{4,5}}=2{{R}_{1,2,3}}\Rightarrow {{I}_{1}}=2{{I}_{2}}}I=2{{I}_{2}}+{{I}_{2}}\Rightarrow {{I}_{2}}=\frac{1}{3}I,{{I}_{1}}=\frac{2}{3}I$

${{I}_{1}}={{I}_{3}}+{{I}_{4}}\xrightarrow{{{R}_{2}}={{R}_{3}}\Rightarrow {{I}_{3}}={{I}_{4}}}{{I}_{1}}=2{{I}_{3}}\Rightarrow {{I}_{3}}={{I}_{4}}=\frac{1}{2}{{I}_{1}}=\frac{1}{3}I$

$\left. \begin{matrix} {{Q}_{1}}={{R}_{1}}I_{1}^{2}t=4\times \frac{4}{9}{{I}^{2}}\times t=\frac{16}{9}{{I}^{2}}t  \\ {{Q}_{2}}={{Q}_{3}}={{R}_{2}}I_{3}^{2}t=8\times \frac{1}{9}{{I}^{2}}\times t=\frac{8}{9}{{I}^{2}}t  \\ {{Q}_{4}}={{R}_{4}}I_{2}^{2}t=6\times \frac{1}{9}{{I}^{2}}\times t=\frac{6}{9}{{I}^{2}}t  \\ {{Q}_{5}}={{R}_{5}}I_{2}^{2}t=10\times \frac{1}{9}{{I}^{2}}\times t=\frac{10}{9}{{I}^{2}}t  \\ \end{matrix} \right\}\Rightarrow {{Q}_{1}}\gt {{Q}_{5}}\gt {{Q}_{2}}={{Q}_{3}}\gt {{Q}_{4}}$