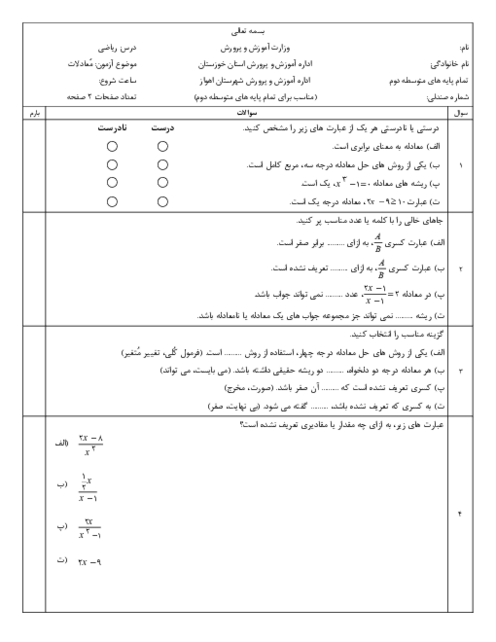
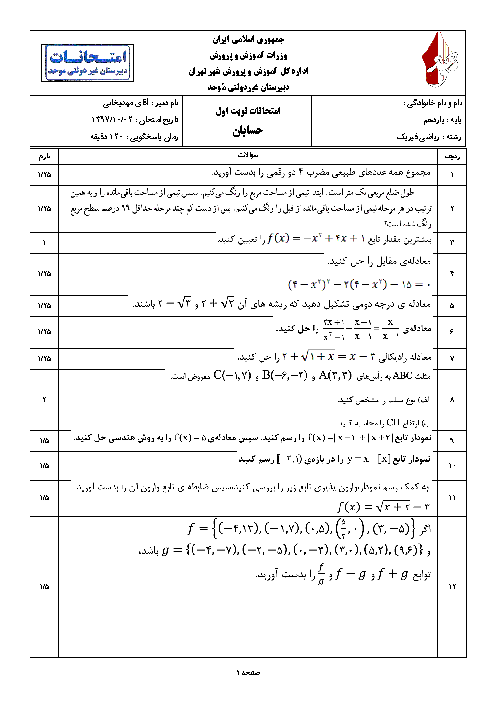
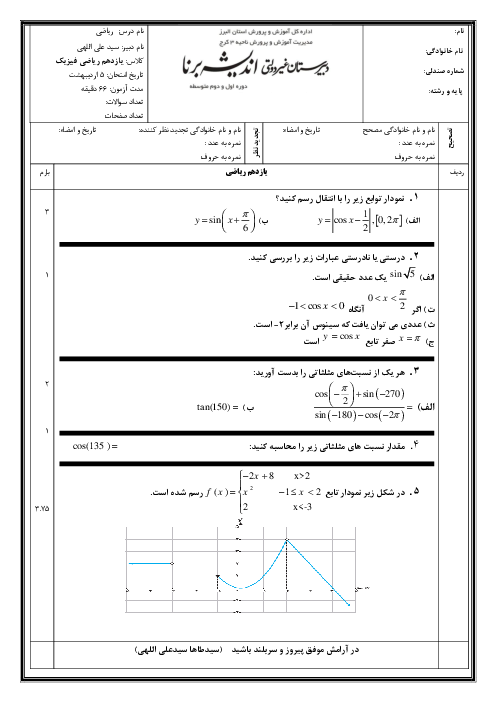
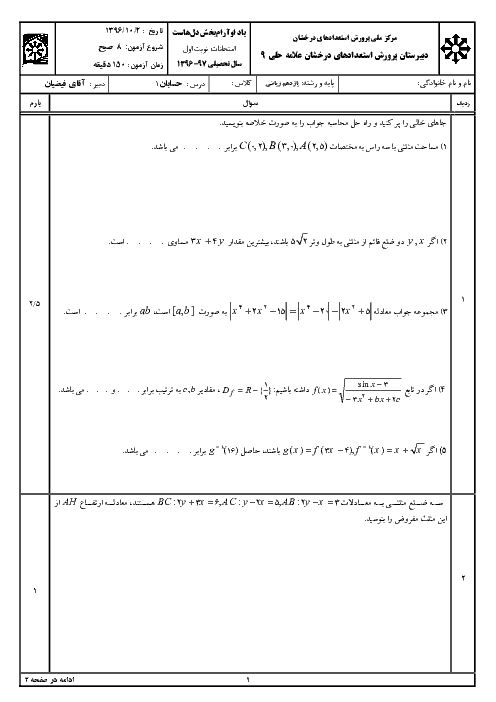
با توجه به اینکه $ \sin \theta = \frac{1}{2} $ و $ \theta $ در ربع دوم قرار دارد، داریم $ \cos \theta = -\frac{\sqrt{3}}{2} $.
برای محاسبه $ \cos \frac{\theta}{2} $ از فرمول نیمزاویه استفاده میکنیم:
$
\cos \frac{\theta}{2} = \pm \sqrt{ \frac{1 + \cos \theta}{2} }
$
با جایگذاری $ \cos \theta = -\frac{\sqrt{3}}{2} $ خواهیم داشت:
$
\cos \frac{\theta}{2} = \pm \sqrt{ \frac{1 - \frac{\sqrt{3}}{2}}{2} } = \pm \sqrt{ \frac{2 - \sqrt{3}}{4} } = \pm \frac{ \sqrt{2 - \sqrt{3}} }{2}
$
از آنجا که $ \theta $ در ربع دوم است، $ \frac{\theta}{2} $ در ربع اول قرار میگیرد و در نتیجه $ \cos \frac{\theta}{2} > 0 $. بنابراین علامت مثبت را انتخاب کرده و جواب نهایی به صورت زیر به دست میآید:
$
\cos \frac{\theta}{2} = \frac{ \sqrt{2 - \sqrt{3}} }{2}
$