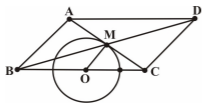
در متوازی‌الاضلاع $ABCD$، نقاط $B$ و $C$ ثابت هستند و ضلع $BA$ طول ثابت $a$ دارد. با تغییر اندازهٔ زاویهٔ $B$، محل برخورد دو قطر متوازی‌الاضلاع روی کدام یک از اشکال هندسی زیر قرار می‌گیرد؟
1 )
دو خط به فاصلهٔ $\frac{a}{2}$ از ضلع $BC$
دایره‌ای به مرکز $O$ نقطهٔ وسط ضلع $BC$ و به شعاع $\frac{a}{2}$
3 )
دایره‌ای به مرکز $O$ نقطهٔ وسط ضلع $BC$ و به شعاع $a$
4 )
دو خط به فاصلهٔ $a$از ضلع $BC$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...