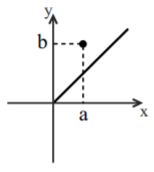
درس 1: مفهوم تابع و بازنماییهای آن
ریاضی (1)
دهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
تابع $f=\left\{ (-1,2),(7,{{m}^{2}}-4m),(m,6),(2,5),(7,5) \right\}$ ، چند نقطه بالای نیمساز ناحیهی اول دارد؟