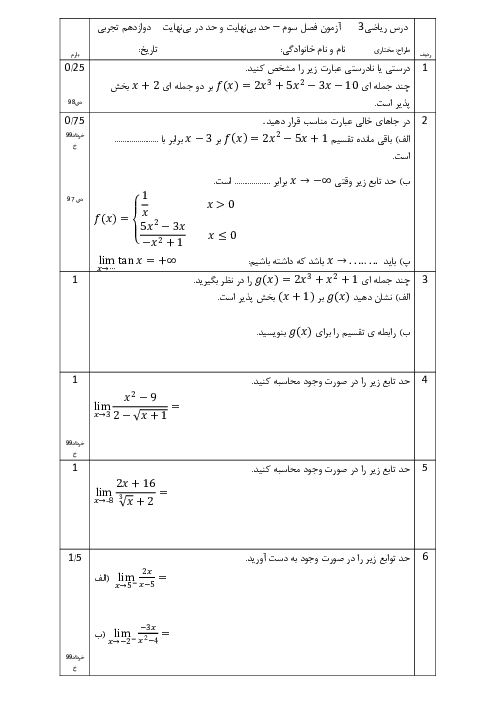
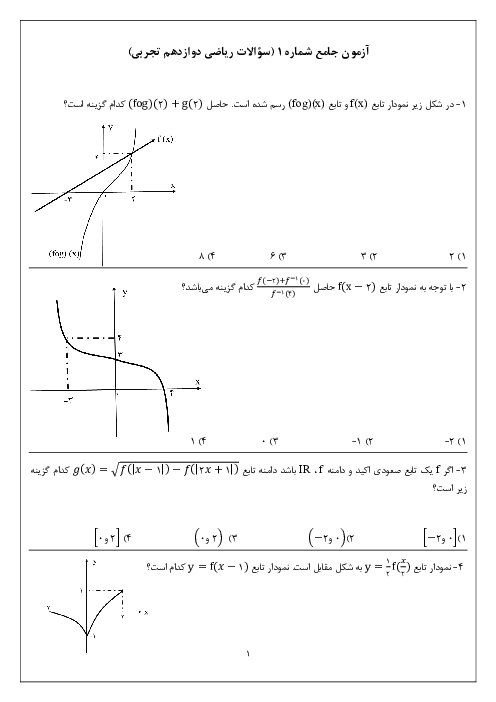
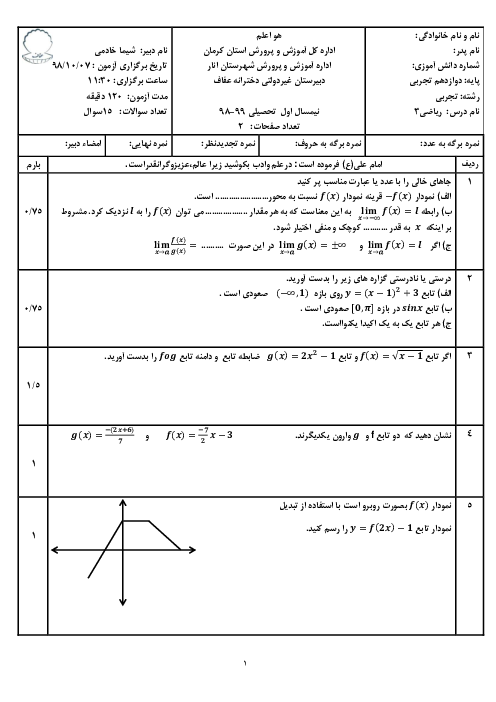
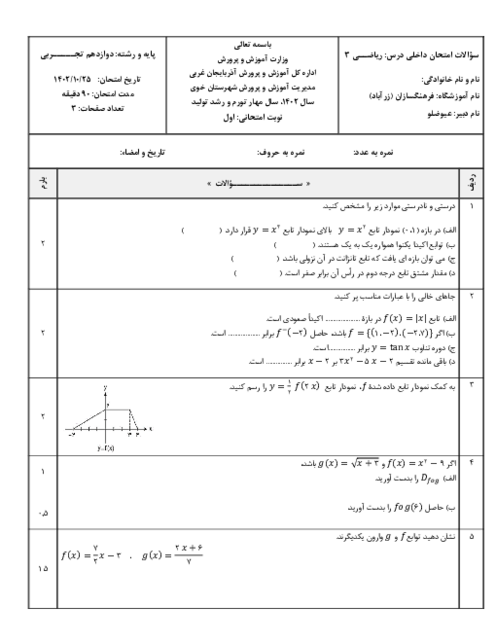
تابع $f(x) = - 2{x^3} + 3{x^2} + 12x - 9$ را در نظر بگیرید:
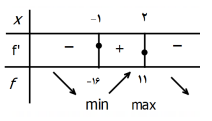
الف) با رسم جدول تغییرات تابع، نقاط ماکزیمم و مینیمم نسبی آن را در صورت وجود مشخص کنید.
ب) مقادیر ماکزیمم مطلق و مینیمم مطلق تابع f در بازه $\left[ {0,3} \right]$ در صورت وجود به دست آورید.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...