مطابق شکل زیر، نیروی F= 0/4kN تحت زاویهٔ 37 درجه به جعبه‌ای به جرم 20 کیلوگرم وارد شده و آن را به اندازهٔ 5 متر روی سطح افقی جابه‌جا می‌کند. اگر تندی اولیهٔ جعبه…

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 3: کار، انرژی و توان فیزیک (1) دهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

مطابق شکل زیر، نیروی F= 0/4kN تحت زاویهٔ 37 درجه به جعبه‌ای به جرم 20 کیلوگرم وارد شده و آن را به اندازهٔ 5 متر روی سطح افقی جابه‌جا می‌کند. اگر تندی اولیهٔ جعبه 10/8 کیلومتر بر ساعت و تندی نهایی آن 18 کیلومتر بر ساعت باشد، اندازهٔ نیروی اصطکاک وارد بر جعبه چند کیلونیوتون است؟ $(\cos {{37}^{\circ }}=0/8)$

1 )

0/288

2 )

0/188

3 )

0/250

4 )

صفر

نمایش پاسخ

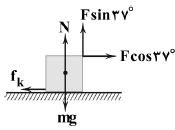
ابتدا تمام نیروهای وارد بر جسم را رسم می‌کنیم و بردار $\overset{\to }{\mathop{F}}\,$ را به دو مؤلفهٔ عمود بر هم تجزیه می‌کنیم. (شکل پایین صفحه)

کار نیروهای عمود بر راستای جابه‌جایی برابر با صفر است. بنابراین مطابق با قضیهٔ کار _ انرژی جنبشی می‌توان نوشت:

$\begin{align}
& {{W}_{t}}={{K}_{2}}-{{K}_{1}}\Rightarrow {{W}_{F}}+{{W}_{{{f}_{k}}}}={{K}_{2}}-{{K}_{1}} \\
& \Rightarrow (F\,\cos {{37}^{\circ }}-{{f}_{k}})d=\frac{1}{2}m(v_{2}^{2}-v_{1}^{2})\xrightarrow[{{v}_{1}}=10/8\frac{km}{h}=3\frac{m}{s},{{v}_{2}}=18\frac{km}{h}=5\frac{m}{s}]{F=0/4kN=400N}(400\times 0/8-{{f}_{k}})\times 5=\frac{1}{2}\times 20({{5}^{2}}-{{3}^{2}}) \\
& \Rightarrow {{f}_{k}}=288N=0/288kN \\
\end{align}$