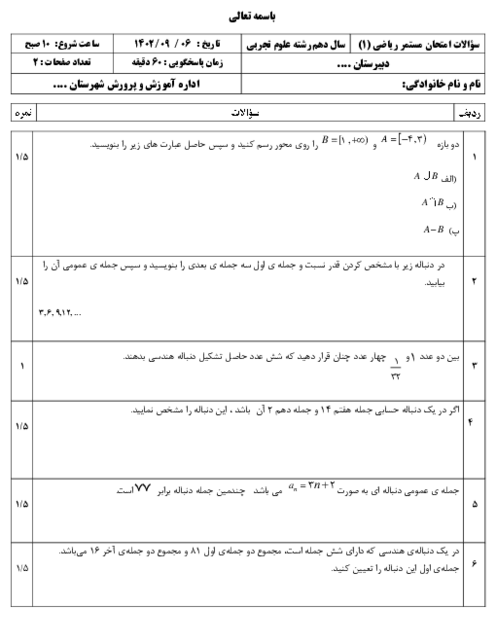
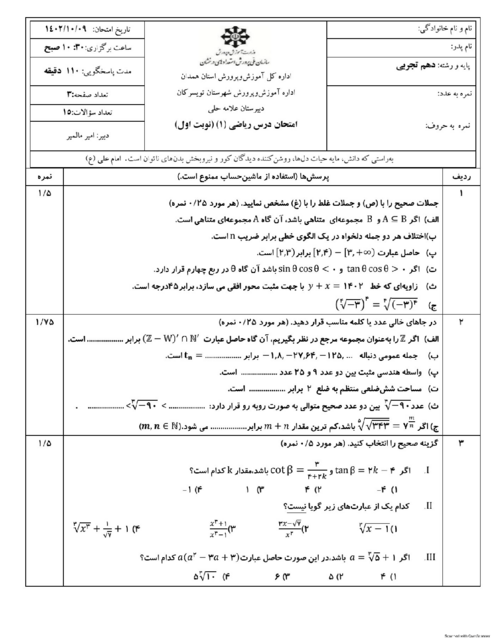
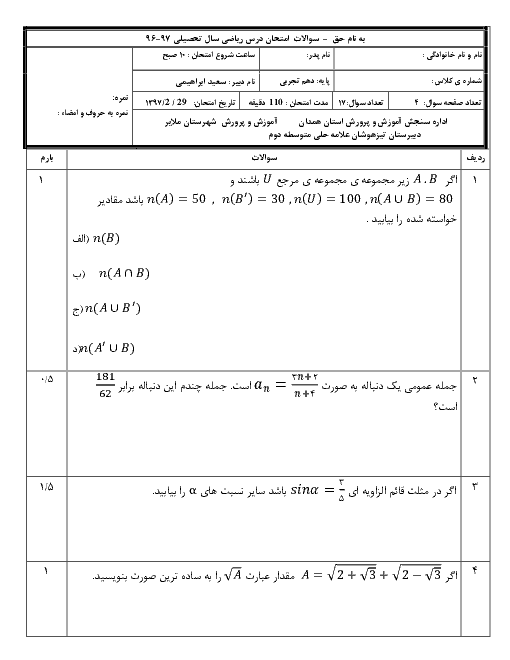
درس 1: معادلۀ درجه دوم و روش‌های مختلف حل آن
ریاضی (1)
دهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
کدام یک از معادلات زیر به ازای تمام مقادیر حقیقی $a$ جواب دارد؟
1 )
$x^{2}-2x+a=0$
2 )
$a^{2}x^{2}+x+1=0$
$x^{2}+(a+1)x+a=0$
4 )
$-x^{2}+ax-1=0$
پاسخ تشریحی :
تحلیل ویدئویی تست
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...