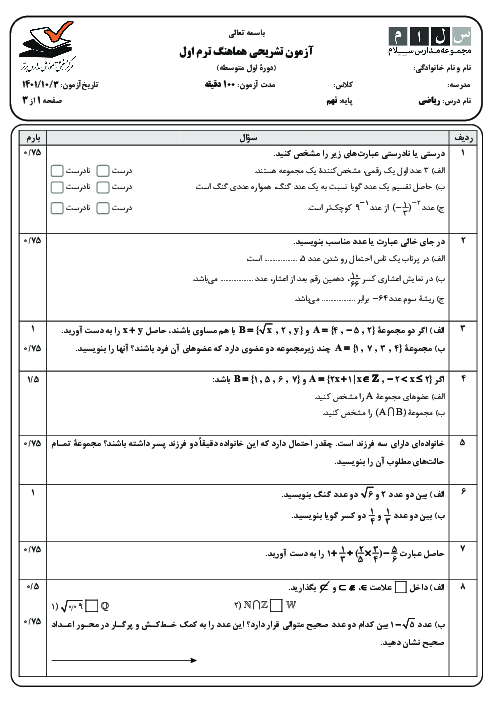
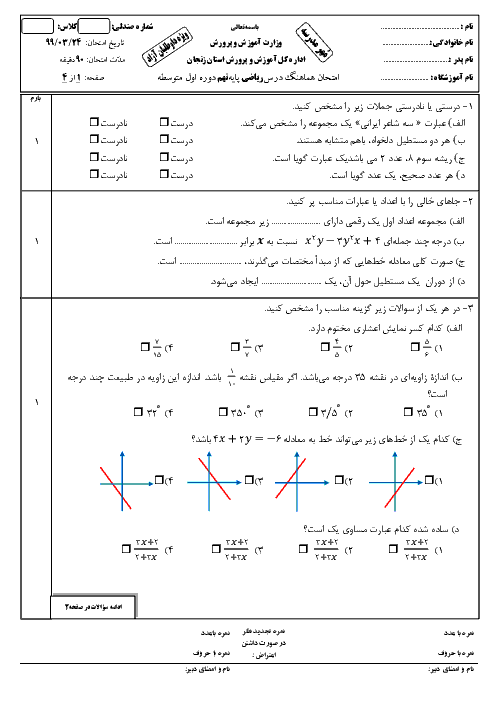
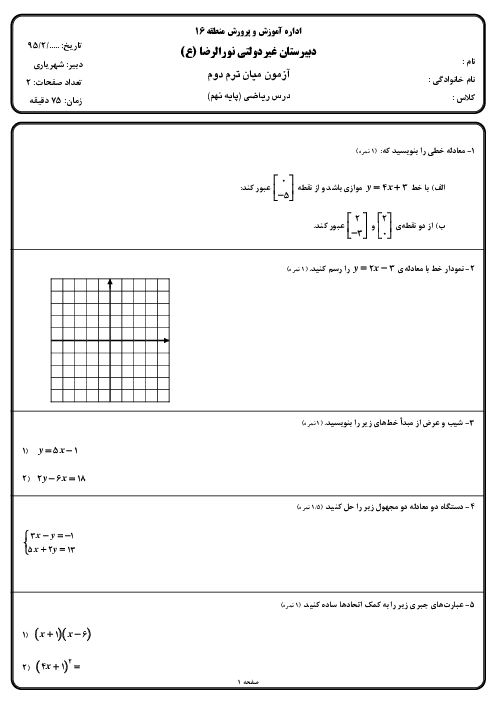
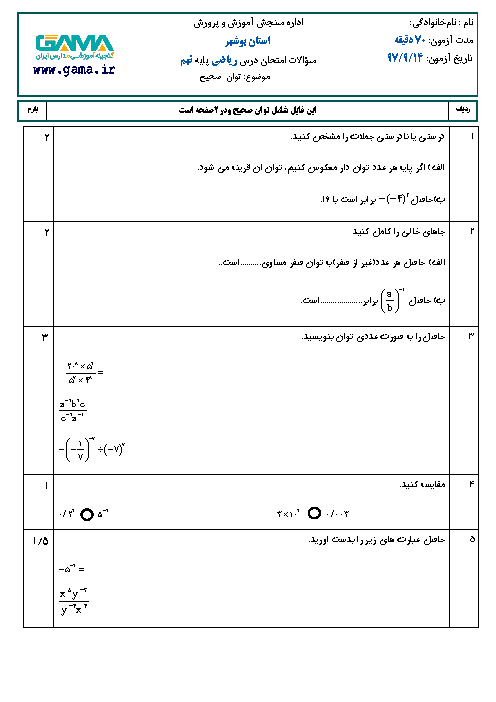
حاصل عبارت زیر بهصورت یک عدد تواندار با توان 6 کدام است؟
$\frac{{{3^5} + {{\left( {\frac{1}{3}} \right)}^{ - 3}} \times 9 + {{\left( {\frac{1}{{27}}} \right)}^{ - 2}} \times \frac{1}{3}}}{{{5^{18}} \times 0/{2^6}}}$
1 )
${\left( {\frac{3}{5}} \right)^6}$
2 )
${\left( {\frac{3}{10}} \right)^6}$
3 )
${\left( {\frac{9}{5}} \right)^6}$
${\left( {\frac{3}{25}} \right)^6}$