نمودار شتاب - زمان متحرکی که در مبدأ زمان از مبدأ مکان با سرعت روی محور می‌گذرد، مطابق شکل زیر است. کدام گزینه در مورد حرکت این متحرک صحیح نیست؟ | فیزیک (3) ریاضی دوازدهم شماره 68918

گاما رو نصب کن!

درحال دریافت اطلاعات ...

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

قسمت 3: حرکت با شتاب ثابت فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

نمودار شتاب - زمان متحرکی که در مبدأ زمان از مبدأ مکان با سرعت $6\frac{m}{s}$ روی محور $x$ می‌گذرد، مطابق شکل زیر است.

کدام گزینه در مورد حرکت این متحرک صحیح نیست؟

1 )

حرکت متحرک همواره در جهت محور $x$ است.

2 )

حرکت ابتدا کندشونده و سپس تندشونده است.

3 )

متحرک جهت حرکتش را یکبار عوض کرده است.

4 )

جابجایی متحرک در کل حرکت 28 متر است.

نمایش پاسخ

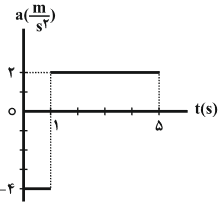
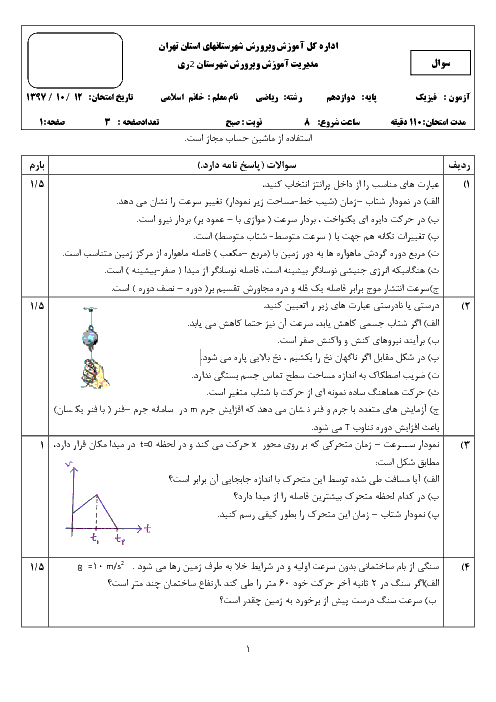
$v(t=0)=+6\frac{m}{s},\Delta v(t=0$ تا $t=1s)=-1\times 4=-4\frac{m}{s}$

$v(t=1s)=6-4=2\frac{m}{s}$

$v(t=1s)=2\frac{m}{s},\Delta v(t=1s$ تا $t=5s)=2\times 4=8\frac{m}{s}$

$v(t=5s)=2+8=10\frac{m}{s}$

متحرک در لحظهٔ $t=0$ با سرعت $6\frac{m}{s}$ در جهت $x$ از مبدأ مکان عبور کرده و تا لحظهٔ $t=1s$ سرعتش به $2\frac{m}{s}$ کاهش یافته است (حرکت کندشونده) سپس با شتاب $2\frac{m}{{{s}^{2}}}$ سرعتش افزایش یافته و به $+10\frac{m}{s}$ رسیده است. (حرکت تند شونده)
- سرعت متحرک به صفر نرسیده و تغییر علامت نداده است، پس تغییر جهت نداریم.
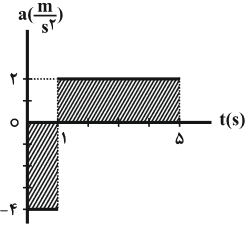
- محاسبه جابه‌جایی توسط رابطهٔ مستقل از شتاب:

$\Delta x=\frac{{{v}_{1}}+{{v}_{2}}}{2}\times \Delta t$

$\Delta {{x}_{1}}(t=0$ تا $t=1s)=\frac{6+2}{2}\times 1=4m$

$\Delta {{x}_{2}}(t=1s$ تا $t=5s)=\frac{2+10}{2}\times 4=24m$

$\Delta {{x}_{T}}=\Delta {{x}_{1}}+\Delta {{x}_{2}}=4+24=28m$