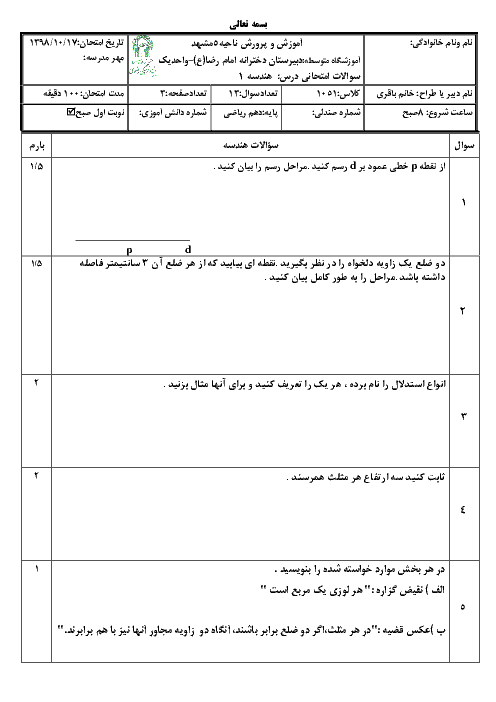
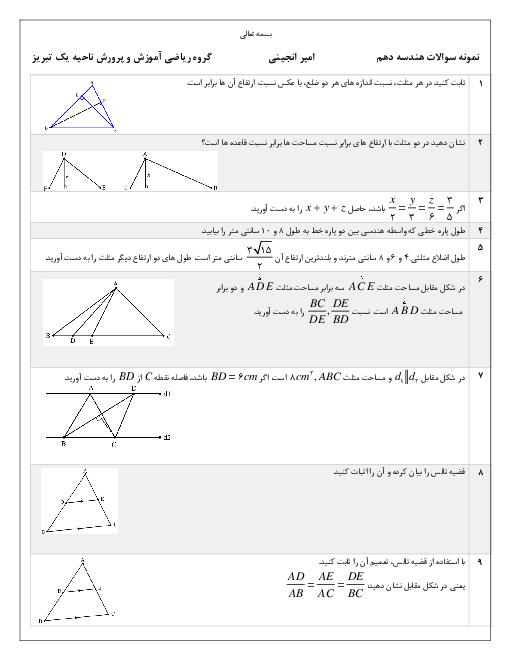
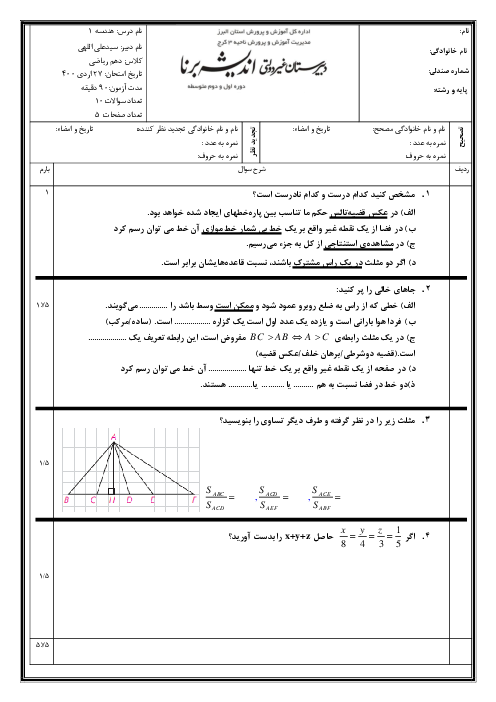
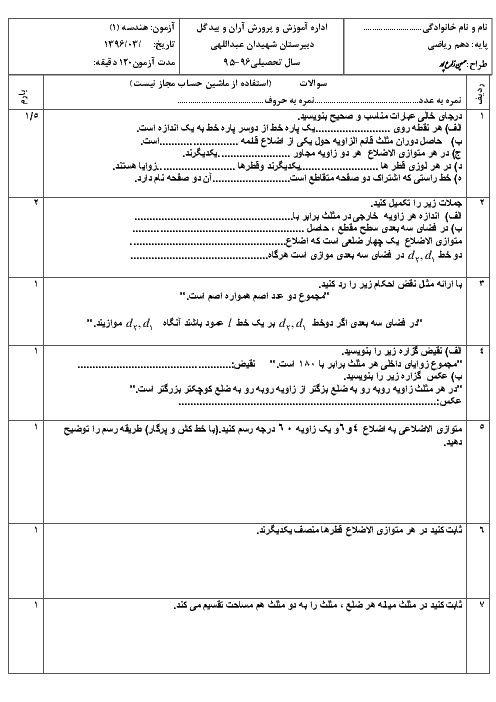
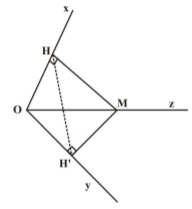
در شكل زير، $xOy$ يک زاويهٔ منفرجه و $Oz$ نيمساز آن است. از نقطهٔ $M$ روی $Oz$، عمودهای $MH$ و $M{H}'$ بر اضلاع زاويهٔ $xOy$ رسم شده است. كدام نامساوی همواره درست است؟
$OH\lt HM\lt OM$
2 )
$MH\lt OH\lt OM$
3 )
$OH\lt OM\lt HM$
4 )
$H{H}'\lt HM\lt OH$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...