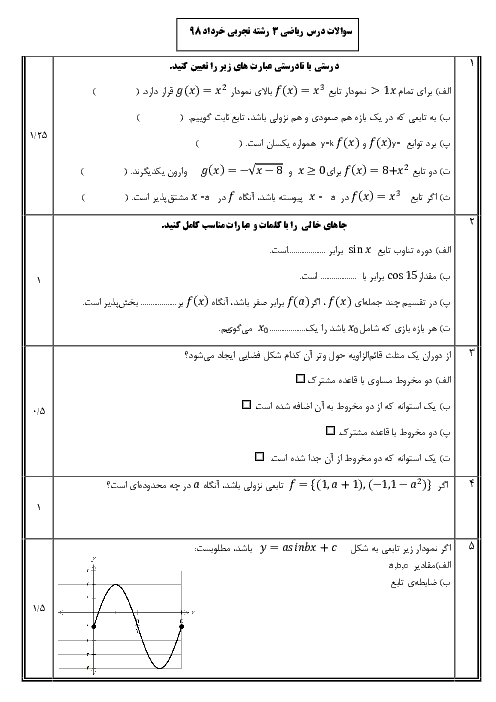
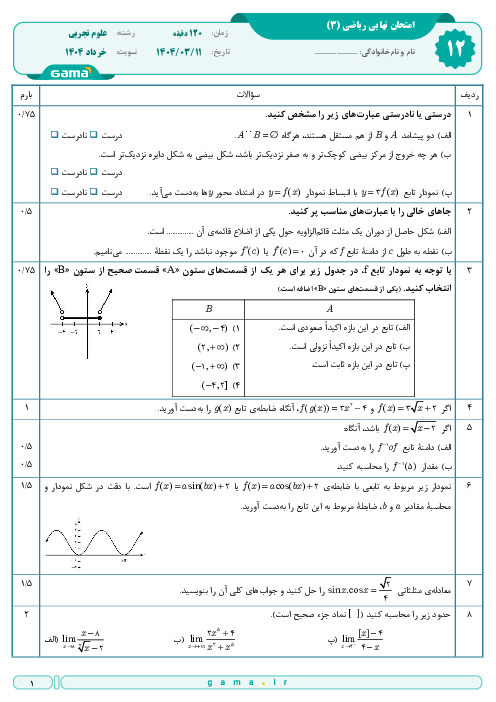
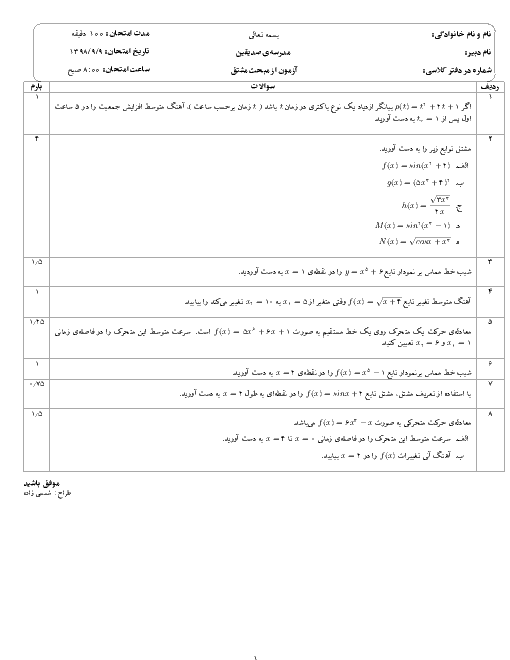
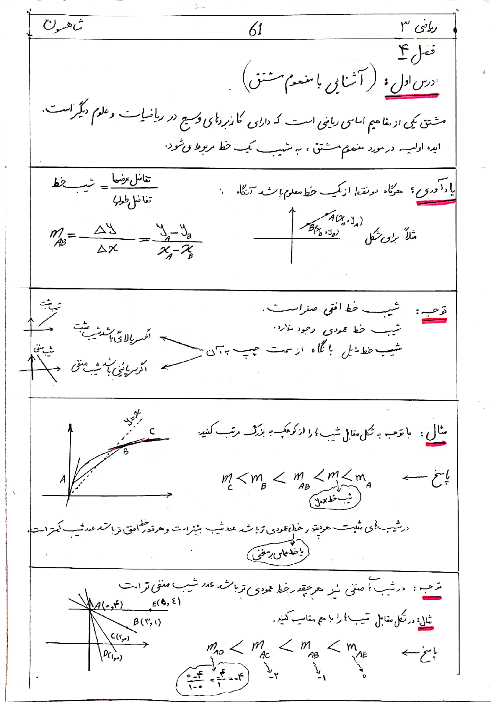
میخواهیم مخزنی به شکل مکعب مستطیل در باز بسازیم که حجم آن $8{{m}^{3}}$ بوده و کف مخزن مربع شکل باشد. قیمت مصالح موردنیاز جهت کف این مخزن برای هر متر مربع $256$ هزار تومان و این قیمت برای دیوارهها در هر متر مربع $250$ هزار تومان است. ابعاد کف مخزن چقدر باشد، تا هزینهی مصالح مصرفی کمترین مقدار ممکن گردد؟
$2/5\times 2/5$
2 )
$2\times 2$
3 )
$\sqrt[3]{4/5}\times \sqrt[3]{4/5}$
4 )
$\sqrt[3]{9}\times \sqrt[3]{9}$
پاسخ تشریحی :
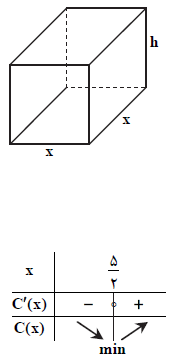
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!