قسمت 3: حرکت با شتاب ثابت
فیزیک (3) تجربی
دوازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
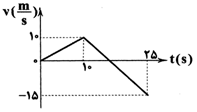
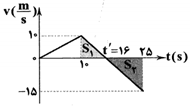
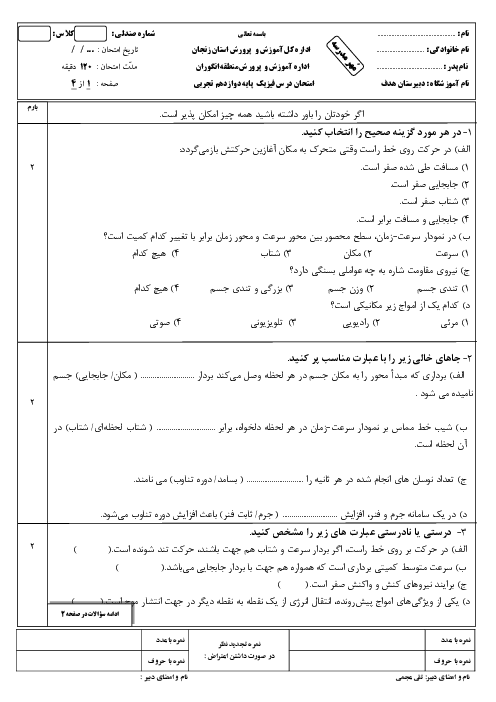
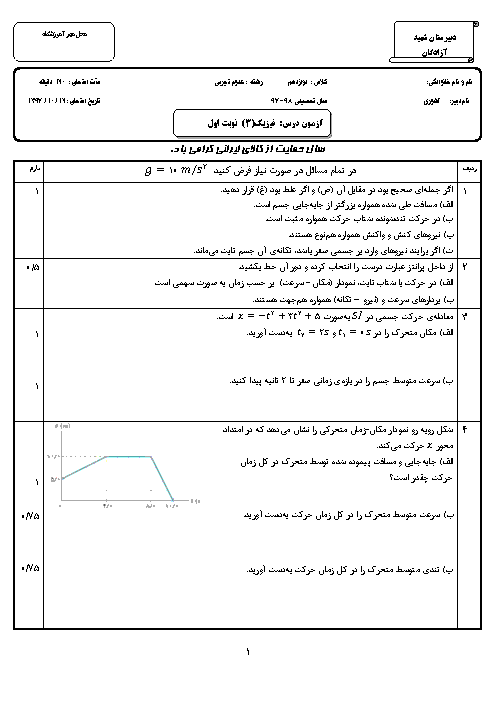
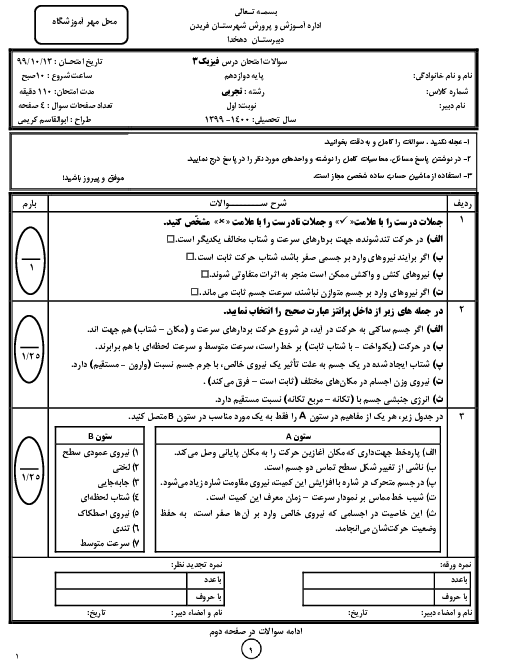
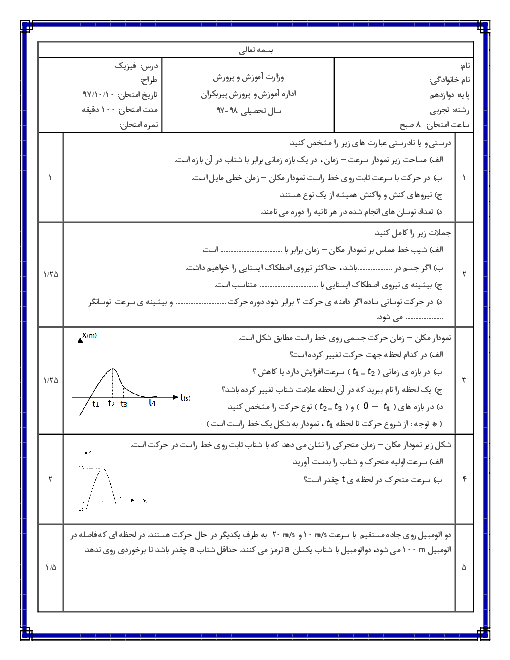
نمودار سرعت - زمان متحرکی که در راستای محور $x$ حرکت میکند، مطابق شکل زیر است. در 25 ثانیهی اول حرکت، در بازهی زمانیای که بردار شتاب متحرک در خلاف جهت محور $x$ است، تندی متوسط متحرک چند متر بر ثانیه میباشد؟