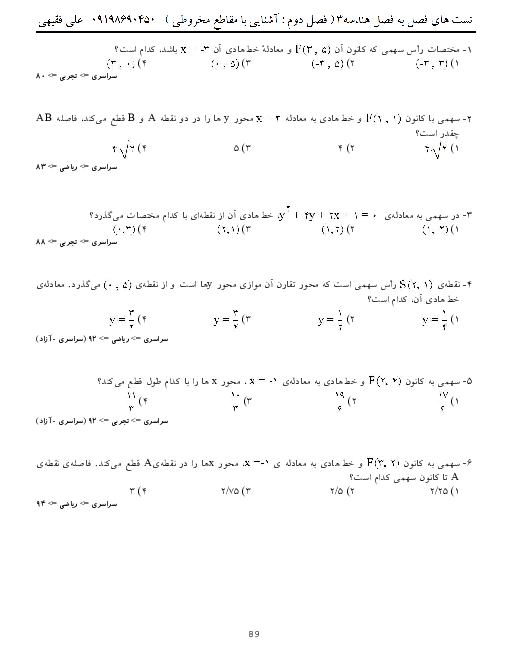
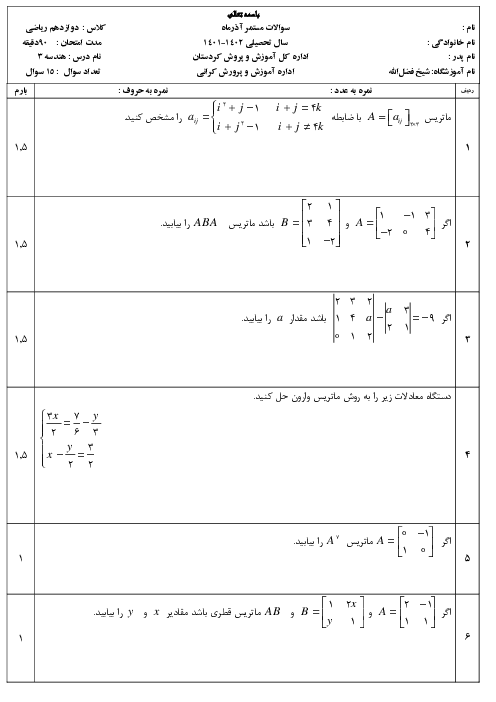
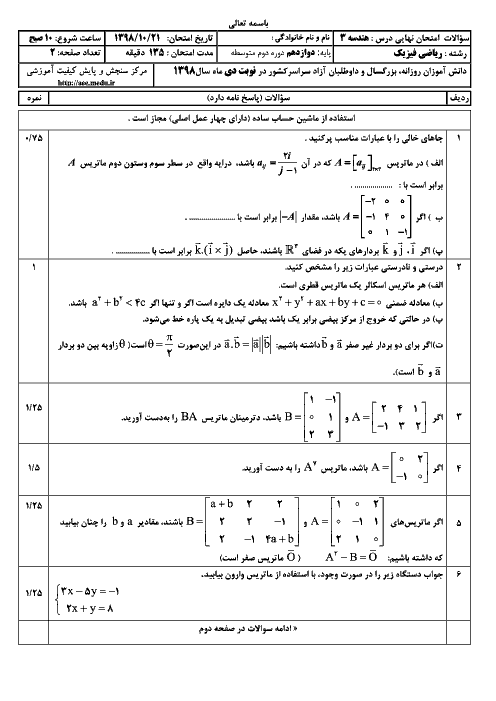
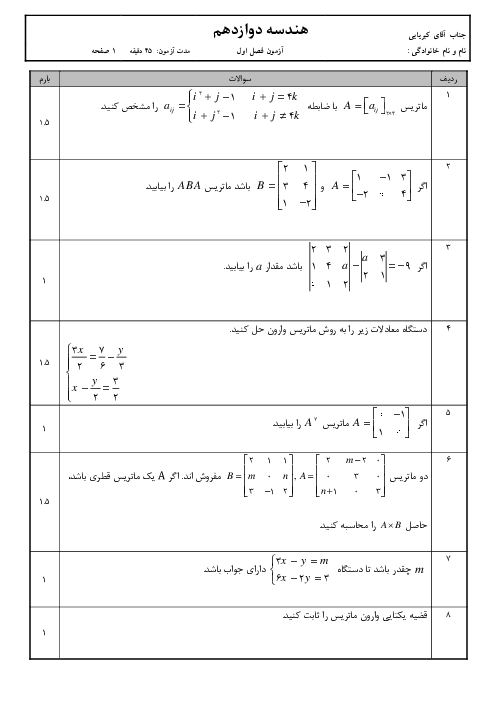
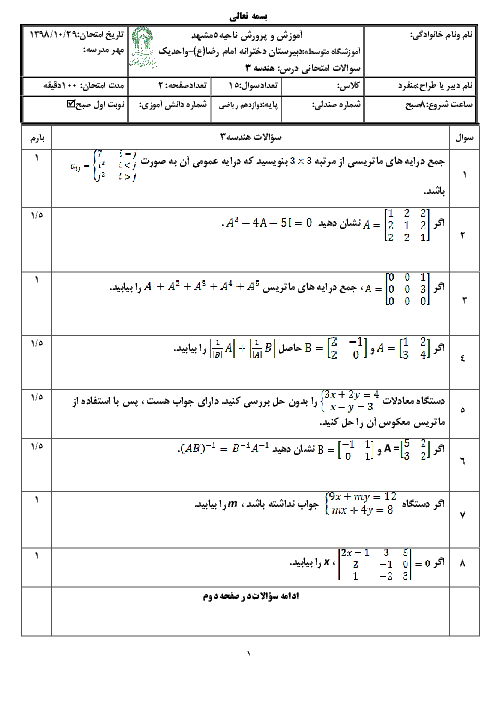
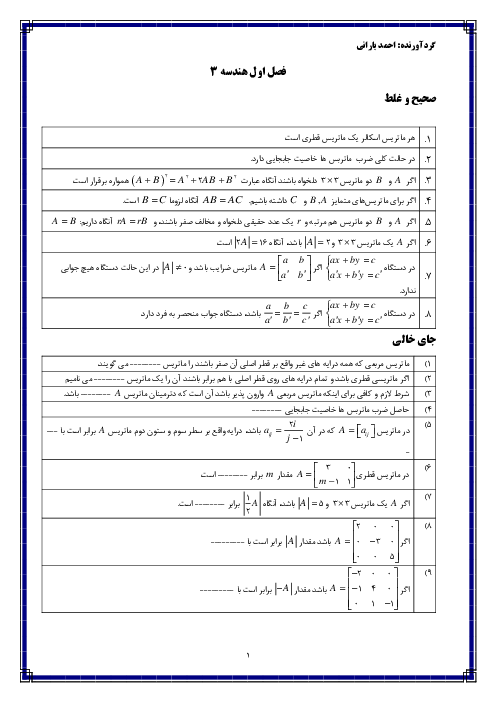
می‌دانیم ${{A}^{2}}+AB$ برابر $A\times (A+B)$ است، یعنی از سمت چپ از $A$ فاکتور گرفتیم. بنابراین داریم:

$\left[ \begin{matrix}
   1 & 3 & 1  \\
   1 & -1 & 2  \\
   3 & 1 & 0  \\
\end{matrix} \right]\times \left( \left[ \begin{matrix}
   1 & 3 & 1  \\
   1 & -1 & 2  \\
   3 & 1 & 0  \\
\end{matrix} \right]\left[ \begin{matrix}
   2 & 1 & 1  \\
   -1 & 0 & 4  \\
   3 & 2 & 5  \\
\end{matrix} \right] \right)$

$=\left[ \begin{matrix}
   1 & 3 & 1  \\
   1 & -1 & 2  \\
   3 & 1 & 0  \\
\end{matrix} \right]\times \left[ \begin{matrix}
   3 & 4 & 2  \\
   0 & -1 & 6  \\
   6 & 3 & 5  \\
\end{matrix} \right]=\left[ \begin{matrix}
   9 & 4 & 25  \\
   \bigcirc  & \bigcirc  & \bigcirc   \\
   \bigcirc  & \bigcirc  & \bigcirc   \\
\end{matrix} \right]$

همان‌طور که می‌بینید مجموع درایه‌های سطر اول برابر $9+4+25=38$ می‌باشد. توجه کنید با نوشتن ${{A}^{2}}+AB$ به صورت $A\times (A+B)$ به جای دوبار انجام عمل ضرب، یک بار ضرب می‌کنیم.